திரவத்தம்பத்தினால் ஏற்படும் அழுத்தம்

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

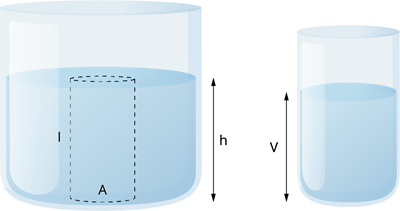
Book Free Demo

ஒரு உயரமான கொள்கலன் திரவத்தால் நிரப்பப்படுகிறது, இதனால் அது ஒரு திரவத்தம்பத்தை உருவாக்குகிறது.

அதன் குறுக்கு வெட்டுப்பரப்பளபை

$A$ என்க.

திரவத்தின் அடர்த்தி

$\rho$ ஆல் குறிக்கப்படுகிறது, மேலும் திரவத்தம்பத்தின் உயரம்

$h$ ஆகும்.

வேறுவிதமாகக் கூறுவதானால், மேல்-நிலை மேற்பரப்பில் இருந்து நீரின் ஆழம்

$h$ ஆகும்.

திரவத்தம்பத்தினால் ஏற்படும் அழுத்தம்

திரவத்தம்பத்தின் அடிப்பகுதியிலுள்ள உந்து விசையானது திரவத்தின் எடைக்கு சமம் என்பதை நாம் அறிவோம். ஆகையால்,

$F = mg \to 1$

திரவத்தின் நிறையானது திரவத்தின் பருமனை அதன் அடர்த்தியால் பெருக்கினால் கிடைக்கும். எனவே:

$m = ρ V \to 2$

எனவே, திரவத்தின் பருமன்:

$\begin{array}{l} V = குறுக்குவெட் டுப் பரப்பளவு (A) \times உயரம் (h) \\ V = A \times h \to 3 \end{array}$

சமன்பாடு

$3$ இல்

$2$ பிரதியிட:

நிறை,

$m = ρ Ah \to 4$

சமன்பாடு (

$4$ ஐ,

$1$ இல் பிரதியிட:

$விசை = mg = ρ Ahg$

இப்போது, அதை அழுத்த சூத்திரத்தில் பயன்படுத்தவும்.

$அழுத்தம் (P) = \frac{உந்துவிசை (F)}{பரப்பளவு (A)} = \frac{mg}{A} = \frac{ρ Ahg}{A} = ρ hg$

எனவே,

$திரவத் தம்பத்தினால் ஏற்படும் அழுத்தம் (P) = ρ hg$

மேலே உள்ள சமன்பாடு ஒரு திரவத் தம்பத்தினால் ஏற்படும் அழுத்தம் ஆனது ஆழம், திரவத்தின் அடர்த்தி மற்றும் ஈர்ப்பு விசையின் முடுக்கம் ஆகியவற்றால் தீர்மானிக்கப்படுகிறது என்பதைக் காட்டுகிறது.

இருப்பினும், அழுத்தத்திற்கான இறுதி சமன்பாடு பகுதி

$A$ என்ற சொல்லைக் கொண்டிருக்கவில்லை. எனவே, ஒரு திரவத்தில் அழுத்தம் ஆழத்தை மட்டுமே சார்ந்துள்ளது.

Example:

$0.9$ மீ திரவத்தம்பையால் செலுத்தப்படும் நீரின் அழுத்தத்தைக் கணக்கிடுங்கள். (நீரின் அடர்த்தி,

$ρ_w\ =$

$1000$ கிகி மீ

$^{-3}$

தீர்வு:

திரவத்தம்பையின் உயரம் அல்லது ஆழம் (

$h$ )

$=$

$0.9$ மீ