PDF chapter test TRY NOW
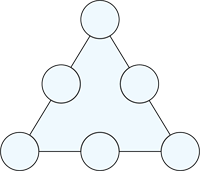
மாய முக்கோணத்தில் எண்களை ஒரு முறை மட்டுமே பயன்படுத்தி ஒவ்வொரு பக்கங்களின் கூடுதலும் சமமாக இருக்குமாறு அமைத்தல் வேண்டும்.
மாய முக்கோணத்தில் 1 முதல் 6 வரை எண்களைப் பயன்படுத்தித் திரும்ப அதே எண்களைப் பயன்படுத்துதல் முக்கோணத்தின் ஒவ்வொரு பக்கங்களின் கூடுதல் சமமாக 12 ஆக வருமாறு அமைக்கவும்.
Example:
மாய முக்கோணத்தில் 1 லிருந்து 6 வரை எண்களைப் பயன்படுத்தி எத்தனை விடைகளைக்கொண்டு வரலாம்?
ஆனால் அனைத்துப் பக்கங்களிலும் ஒரே கூடுதல் வரவேண்டும்.
நான்கு சாத்தியமான தீர்வுகள் பின்வருமாறு:
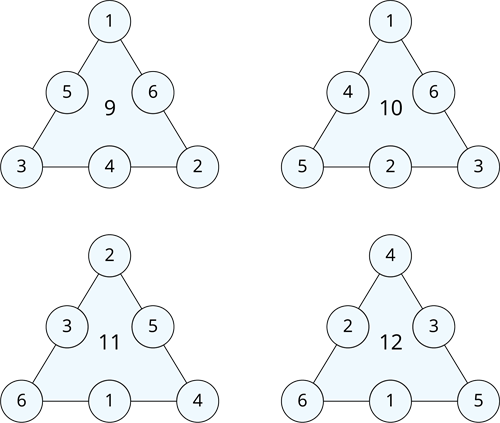
பக்க நீளத்தை 9 ஆக மாற்றுவதற்கான நுட்பம்:
1. முக்கோணத்தின் மூலைகளில் கீழ் எண்களை 1, 2 மற்றும் 3 வைக்கவும்.
2. இரண்டு சிறிய (1 மற்றும் 2 மூலை ஏற்பாடுகளுக்கு இடையில் மிகப்பெரிய எண்ணை6 வைக்கவும்.
3. மீதமுள்ள நடுத்தர எண்கள் 4 மற்றும் 5 ஆக இருக்கும்.
4. குறைந்தபட்ச தொகை 9 ஆக பக்க நீளத்தை அடைய, 3 மற்றும் 2 க்கு இடையில் 4 ஐ வைக்க வேண்டும் மற்றும் 1 மற்றும் 3 க்கு இடையில் 5 ஐ வைக்க வேண்டும்.
5. எனவே, நாங்கள் மாய முக்கோணத்தை 9 அலகுகள் கொண்ட குறைந்த பக்க நீளத்துடன் உருவாக்கினோம்.
பக்க நீளத்தை 11 ஆக மாற்றுவதற்கான நுட்பம்:
1. முக்கோணத்தின் மூலைகளில் 2, 4 மற்றும் 6 இரட்டை இலக்கங்களை வைக்கவும்.
2. இரண்டு சிறிய 2 மற்றும் 4 மூலை ஏற்பாடுகளுக்கு இடையில் இரண்டாவது பெரிய எண்ணை 5 வைக்கவும்.
3. மீதமுள்ள எண்கள் 1 மற்றும் 3 ஆக இருக்கும்.
3. மீதமுள்ள எண்கள் 1 மற்றும் 3 ஆக இருக்கும்.
4. பக்க நீளத்தை 11 ஆக அடைய நாம் 1 ஐ 6 மற்றும் 4 க்கு இடையில் வைக்க வேண்டும் மற்றும் 3 ஐ 6 மற்றும் 2 க்கு இடையில் வைக்க வேண்டும்.
5. எனவே, நாங்கள் மாய முக்கோணத்தை 11 அலகுகள் கொண்ட குறைந்த பக்க நீளத்துடன் உருவாக்கினோம்.
இப்போது மற்ற இரண்டு மாய முக்கோணங்களுக்கான நுட்பங்களை நிறுவ முயற்சிக்கவும் மற்றும் அதன் விளைவுகளை ஆராயவும்.
Important!
மாய முக்கோணத்தின் சுழற்சிகளும் பிரதிபலிப்புகளும் தனித்துவமான தீர்வுகளாக கருதப்படவில்லை. மாய முக்கோணத் தீர்வு ஒவ்வொன்றும் இரண்டு சுழற்சிகளைக் கொண்டிருக்கும், இவை ஒவ்வொன்றும் ஒரு பிரதிபலிப்பைக் கொண்டிருக்கும். ஒவ்வொரு தீர்வுக்கும் 6 சாத்தியமான நோக்குநிலைகள் உள்ளன.
பக்க நீளம் 9 இன் சாத்தியமான அனைத்து 6 நோக்குநிலைகளையும் பார்ப்போம்.
பக்க நீளம் 9 இன் சாத்தியமான அனைத்து 6 நோக்குநிலைகளையும் பார்ப்போம்.
Register for free to see more content