PDF chapter test TRY NOW
இரு வெட்டும் கோடுகளால் அடுத்துள்ள கோணங்கள், நேரிய கோண இணைகள், குத்தெதிர்க் கோணங்கள் போன்றவை அமைகின்றன. அவற்றைப் பற்றி விரிவாகக் காண்போம்.
அடுத்துள்ள கோணங்கள்:
பொதுவான ஒரு முனை, பொதுவான கதிர் கொண்ட வெவ்வேறு உட்பகுதிகளைக் கொண்ட இரண்டு கோணங்கள் அடுத்துள்ள கோணங்கள் எனப்படும்.
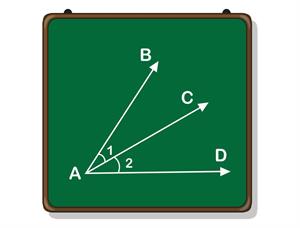
Example:
இதை நாம் ஒரு பீட்சாவை வைத்து பரிசோதித்து அறிந்து கொள்வோம்.
இதிலுள்ள கோணங்கள் \(\angle AOC\), \(\angle AOB\) மற்றும் \(\angle BOC\).
1. \(O\) ஆனது பொது முனை.
2. \(\overrightarrow{OB}\) ஆனது \(\angle AOB\) மற்றும் \(\angle BOC\) க்கான பொதுவான கதிர் ஆகும்.
3. \(\angle AOB\) மற்றும் \(\angle BOC\) பொதுவான உட்பகுதிகளைக் கொண்டிருக்கவில்லை.
எனவே, \(\angle AOB\) மற்றும் \(\angle BOC\) அடுத்தடுத்த கோணங்கள் ஆகும்.
நேரிய கோண இணை:
மிகை நிரப்பு கோணங்களாக இருக்கும் அடுத்துள்ள கோணங்கள் நேரிய கோண இணைகள் எனப்படும். அதாவது, ஒரு கோட்டின் மீது ஏதேனும் ஒரு புள்ளியில் அமையும் கோணங்களின் கூடுதல் \(180^\circ\) ஆக இருப்பின் அவை நேரிய கோண இணை எனப்படும்.
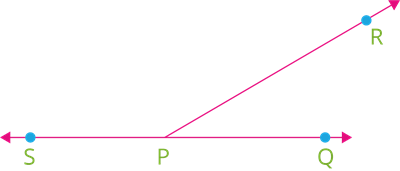
இங்கே, \(\angle SPR + \angle RPQ = 180^\circ\). ஏனெனில், இவை ஒரே நேர்க்கோட்டில் அமைந்த கோணங்கள். எனவே, \(\angle SPR\) மற்றும் \(\angle RPQ\) நேரிய இணை கோணங்கள் ஆகும்.
நேரிய கோண இணைகள் – மேலும் சில முடிவுகள்:
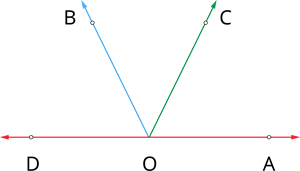
\(\angle DOB\), \(\angle BOC\) மற்றும் \(\angle COA\) ஆகியவை ஒரே கோட்டில் அமைந்த கோணங்கள்.
எனவே, \(\angle DOB + \angle BOC + \angle COA = 180^\circ\).
ஒரு நேர்கோட்டின் மீதுள்ள ஏதேனும் ஒரு புள்ளியில் அமையும் கோணம் \(180^\circ\) ஆகும்.
ஒரே புள்ளியில் இருந்து பல கதிர்கள் தோன்றினால் கோணம் என்னவாக இருக்கும் என்று சிந்தியுங்கள்!
அனைத்து கதிர்களும் ஒரு புள்ளியில் இருந்து தொடங்குகின்றன. எனவே, ஒரு புள்ளியைச் சுற்றியுள்ள அனைத்துக் கோணங்களின் கூட்டுத்தொகை \(360^\circ\) இருக்கும்.
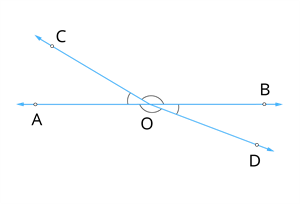
\(\angle AOC + \angle BOC + \angle BOD + \angle AOD\)
\(= 180^\circ + 180^\circ\)
\(= 360^\circ\)
ஒரு புள்ளியில் அமையும் அனைத்துக் கோணங்களின் கூடுதல் \(360^\circ\) ஆகும்.
குத்தெதிர்க் கோணங்கள்
இரு கோடுகள் ஒன்றையொன்று வெட்டிக்கொள்ளும்போது உருவாகும் இரு சோடி அடுத்தமையாக் கோணங்கள், குத்தெதிர்க் கோணங்கள் என அழைக்கப்படும்.
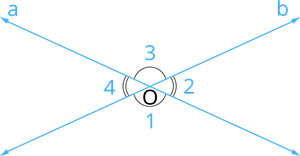
இங்கே \(\angle 1\) இன் அடுத்துள்ள கோணங்கள் \(\angle 2\) மற்றும் \(\angle 4\) எனில், \(\angle 3\) என்னவாக இருக்கும்?
\(\angle 3\) ஆனது \(\angle 1\) க்கு நேர் எதிரில், ஒரே புள்ளியில் இரு கோடுகள் வெட்டிக்கொள்வதால் உருவாகின்றது. எனவே, இவ்விரு கோணங்களும் குத்தெதிர்க் கோணங்கள் ஆகும். இதே போல், \(\angle 2\) மற்றும் \(\angle 4\) உம் குத்தெதிர்க் கோணங்கள் ஆகும்.
இக்குத்தெதிர்க் கோணங்கள் சமமாக இருக்கும்.
\(\angle 1 = \angle 3\)
\(\angle 2 = \angle 4\)
Important!
குத்தெதிர்க் கோணங்கள் சமமாக இருக்கும்.
Register for free to see more content