PDF chapter test TRY NOW
தகு உட்கணம் (Proper subset)
\(A\) மற்றும் \(B\) இரு கணங்கள் என்க. கணம் \(A\) இல் உள்ள அனைத்து உறுப்புகளும் \(B\) இல் இருக்க வேண்டும். ஆனால், \(B\) இல் குறைந்தபட்சம் ஒரு உறுப்பாவது \(A\) ஐ விட அதிகமாக இருக்க வேண்டும் \((A ≠ B)\). இவ்வாறு உள்ள கணம் தகு உட்கணம் எனப்படும். இதை \(A \subset B\) என எழுதலாம்.
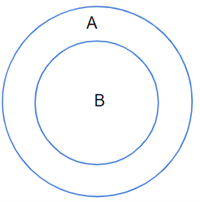
Example:
\(A = \{2, 7, 8, 9\}\) மற்றும் \(B = \{2, 5, 7, 8, 9, 10\}\)
\(\{2, 7, 8, 9\} \subset \{2, 5, 7, 8, 9, 10\}\)
\(A \subset B\)
அடுக்குக் கணம் (Power Set):
\(A\) என்ற கணத்தின் அனைத்து உட்கணங்களையும் கொண்ட கணம், அக்கணத்தின் அடுக்குக் கணம் எனப்படும். இதனை \(P(A)\) எனக் குறிக்கலாம்.
Example:
\(A = \{3, 5\}\) எனில் \(A\) இன் அடுக்குக் கணத்தைக் காண்க.
\(A\) இன் உட்கணங்கள் \(\{\}, \{3\}, \{5\}, \{3, 5\}\).
\(A\) இன் அடுக்குக் கணம், \(P(A) = \{\{\}, \{3\}, \{5\}, \{3, 5\}\}\).
Important!
1. \(n(A) \le n [P(A)]\)
2. \(n(A) = m\) எனில், உட்கணங்களின் எண்ணிக்கை \(n [P(A)] = 2^m\).
3. கணம் \(A\) இன் தகு உட்கணங்களின் எண்ணிக்கை \(n [P(A)] - 1= 2^m - 1\).
Register for free to see more content