PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demo என்பதன் விடையைப் பார்த்தால் ஈவு மற்றும் மீதி .
மேலும், இங்கு என்பது வகுபடும் எண் , என்பது வகுத்தி , என்பது ஈவு, மற்றும் என்பது மீதி.
எனவே, இதனை அல்லது
வகுபடும் எண் \(=\) (வகுத்தி \(×\) ஈவு) \(+\) மீதி என எழுதலாம்.
இயற்கணிதத்ததில் ஒரு பல்லுறுப்புக் கோவையை மற்றொரு பல்லுறுப்புக் கோவையால் நீள்வகுத்தல் முறையைப் பயன்படுத்தி வகுக்கலாம்.
அதனைப் பற்றி காணலாம்.
Example:
இங்கு மற்றும் .
\((2x^3 + x^2 +x) ÷ x\)
\(=\) \(\frac {2x^3}{x}+\) \(\frac{x^2}{x}+\)\(\frac{x}{x}\)
\(=\) \(2x^2\) \(+\) \(x\) \(+\) \(1\).
இங்கு, \((2x^3 + x^2 +x)\) என்பது வகுபடும் கோவை, \(x\) என்பது வகுத்தி, \(2x^2\) \(+\) \(x\) \(+\) \(1\) என்பது ஈவு மற்றும் \(0\) என்பது மீதி.
மேலும், \(q(x)\) என்ற கோவையுடன் \(p(x)\) என்ற கோவை மீதியின்றி வகுபடுவதைக் காணலாம்.
Example:
\(p(x) =\) \(3x^2 + x + 1\) \(\div\) \(q(x)= x\) மதிப்பு காணலாம்.
\((3x^2 + x + 1) ÷ x\) \(=\) \((3x^2 ÷ x)\) \(+ (x ÷ x)\) \(+ (1 ÷ x)\)
\(= 3x + 1 + \frac{1}{x}\).
\((1)\) ஆனது \(x\) ஆல் வகுபடாது,
எனவே, இதனைக் கீழ்க்கண்டவாறு எழுதலாம்.
\(3x^2 + x + 1\) \(=\) \((3x^2 + x)\) \(+1\)
\(((3x +1) (x)) +1\)
\(((3x +1) × x) +1\)
\(3x^2 + x + 1 = \) \(((3x +1) × x) +1\)
இங்கு, \(3x+1\) என்பது ஈவு மற்றும் \(1\) என்பது மீதி. எனவே, \(x\) என்பது \(3x^2 + x + 1\) இன் காரணி அல்ல.
Example:
\(3x^3 – 5x^2 + 10x – 3\) என்பதை \(3x + 1\) ஆள் நீள் வகுத்தல் முறையில் வகுக்கலாம்.
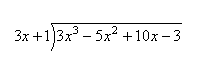
\(3x^3\) ஐ \(3x\)-ஆல் வகுக்கக் கிடைப்பது \(x^2\). இதனை மேலே எழுதவும்.
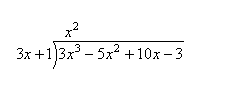
\(x^2\) ஐ \(3x + 1\) உடன் பெருக்கி வரும் \(3x^3 + 1x^2\) ஐக் கீழே எழுதவும்.
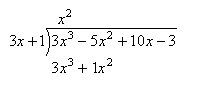
கீழே எழுதிய எண்ணின் குறியை மாற்றி கூட்டவும். "\(+10x – 3\)" ஐ அதே குறியுடன் கீழே எழுத \(– 6x^2 + 10x – 3\) கிடைக்கும்.
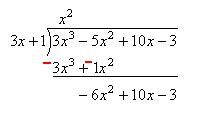
இப்பொழுது \(– 6x^2\) ஐ \(3x\) ஆல் வகுக்க கிடைக்கும் \(– 2x\) ஐ மேலே எழுதவும்.
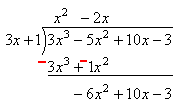
\(– 2x \times 3x + 1\) \(=\)\(– 6x^2 – 2x\) என்ற விடையைக் கீழே எழுதி, அதன் அடையாளத்தை மாற்றி கூட்டவும். \(– 3\) குறியை மாற்றாமல் கீழே இறக்கவும்.
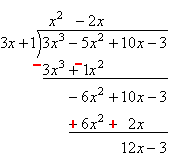
\(12x\) ஐ \(3x\) வகுக்க கிடைக்கும் மீதி \(+4\) ஐ மேலே எழுதவும்.
\(4 \times 3x + 1=12x + 4\) என்ற விடையைக் கீழே எழுதி அடையாளத்தை மாற்றிக் கூட்ட வேண்டும்.
Register for free to see more content