PDF chapter test TRY NOW
வடிவியல் என்பது கிரேக்கத்தில் 'ஏர்த் மேயசுரேமெண்ட் 'என குறிப்பிடப்படுகிறது , இது ஒரு கணிதவியலின் ஒரு பிரிவு அவற்றில் உள்ள பண்புகள் மற்றும் உறவுகள் புள்ளி, கோடு, பரப்பு, திண்மம், மற்றும் உயர் பரிமாணத்தின் ஒப்புமைகள் .
ஒரு குறிப்பிட்ட நிலை அல்லது இடம் என்பது மேற்பரப்பு மற்றும் தளத்தில் உள்ள வரையறுக்கபட்ட புள்ளியாகும் .
மேற்கண்ட படத்தில் இருந்து \(A\) மற்றும் \(B\) என்பன புள்ளிகள் ஆகும்.
ஒரு புள்ளி என்பது கண்ணுக்கு புலப்படாதவை இவற்றை கொண்டு இடம் மற்றும் நிலை திர்மானிக்கப்படுகிறது மேலும் இவற்றை நீட்டிக்க இயலாது . ஒவ்வொரு இடம் மற்றும் நிலையின் பெயரிட ஆங்கில எழுத்துக்களைப் பயன்படுத்தலாம் .
Example:
புள்ளி மற்றும் பெயரிடும் முறையைப் பயன்படுத்தி(\(A\), \(B\), \(C\), \(D\) மற்றும் \(E\)) ஐந்து இடங்களை வரைபடத்தில் குறிப்பிடலாம் .
இரு புள்ளிகளுக்கு இடையே கோடு வரையப்பட்டால் அவை கோட்டுத்துண்டு எனப்படும் .
மேற்கண்ட படத்தில் இருந்து கோட்டுப்பகுதியானது \(AB\) மற்றும் அவற்றை என குறிப்பிடலாம் .
இரு புள்ளிகளுக்கு இடையே உள்ள தொலைவை வரையறுக்க கோட்டுத்துண்டு பயன்படுகிறது.
Example:
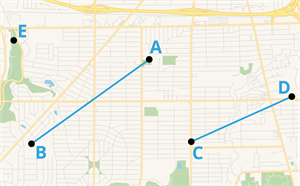
கோட்டுத்துண்டு மற்றும் பெயரிடும் முறையைப் பயன்படுத்தி (\(A\), \(B\), \(C\), \(D\) மற்றும் \(E\)) என்ற ஐந்து கோட்டுத்துண்டுகளை வரைப்படத்தில் குறிப்பிடலாம் . இரு புள்ளிகளுக்கிடையே உள்ள தொலைவு \(A\) மற்றும் \(B\) கோட்டுத்துண்டாக படத்தில் காட்டப்பட்டுள்ளது \(A\) மற்றும் \(B\). இதேப்போன்று , இரு புள்ளிகளுக்கிடையே உள்ள தொலைவு \(B\) மற்றும் \(E\), \(C\) மற்றும் \(D\) கோட்டுத்துண்டாக படத்தில் காட்டப்பட்டுள்ளது .
முடிவற்ற எல்லைகளை கொண்ட இரு புள்ளிகளை இணைத்து வரையப்பட்ட கோடு .இக்கோட்டுத்துண்டானது இருதரப்பு அம்பு கொண்டு பெயரிடப்படுகிறது.
மேற்கண்ட படத்தில் இருந்து \(AB\) என்பது கோட்டுத்துண்டு மற்றும் அல்லது எனப் பெயரிடப்பட்டுள்ளது .
Example:
\(100\) ஓடுதளம் மேற்கூறிய கருத்தை கொண்ட கோடு. ஒரு ஓடுதளத்தில் உள்ள கோடானது தொடக்கமும் முடிவும் அற்ற ஒரு கோட்டுத்துண்டாகும்.
மூன்று மற்றும் அதற்கு மேற்பட்ட புள்ளிகள் ஒரே கோட்டில் அமையுமானால் அவை நேர்கோட்டு புள்ளிகள் எனப்படும் .
மேற்கண்ட படத்தில் இருந்து \(A\), \(B\) மற்றும் \(C\) என்பது நேர்கோட்டு புள்ளிகள் ஆகும்.இவை ஒரே கோட்டில் அமைந்ததால் நேர்கோடு புள்ளிகள் எனப்படும்.
Example:
நேர்கோட்டு கருத்தின் அடிப்படையில் தண்ணீர் குவலைகளை வரிசையாக அடுக்குக.
கோடுகளின் ஒரு முனை முடிவுற்று மறுமுனை முடிவுறாமல் தொடர்ந்தால் அக்கோடுகள் கதிர்கள் என அழைக்கப்படும் .
கதிரின் நிலையாக உள்ள புள்ளி உச்சி எனப்படும். மறுமுனை ஒரு பரிமான சுழற்சி கொண்டு இருக்கும்.
மேற்கண்ட படத்தில் இருந்து \(AB\) என்பது கதிர் மற்றும் இதனை எனக் குறிப்பிடுகிறோம்.
Example:
சாலையின் ஒரு முனையில் இருந்து டார்ச் லைட் பயன்படுத்தினால் அதன் ஒலியின் பாதை மறுமுனையை நோக்கி இருக்கும்(கோட்டுத்துண்டு). ஒலியின் முடிவு புள்ளியை கூற முடியாது. இந்த கோட்டுப்பகுதி கதிர் எனப்படும்.
Register for free to see more content