PDF chapter test TRY NOW
A trigonometric identity is an equation containing trigonometric ratios of an angle that is true for all values of the angle(s) involved.
Fundamental identities of trigonometry:
(1) \sin^2 \theta + \cos^2 \theta = 1
(2) 1 + \tan^2 \theta = \sec^2 \theta
(3) 1 + \cot^2 \theta = \text{cosec}^2\: \theta
We will prove these basic trigonometric identities.
\sin^2 \theta + \cos^2 \theta = 1
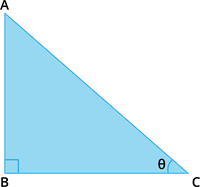
Consider a right triangle ABC with angle \theta.
\sin \theta = \frac{AB}{AC} - - - - - (I)
\cos \theta = \frac{BC}{AC} - - - - - (II)
By Pythagoras theorem:
AB^2 + BC^2 = AC^2
Divide by AC^2 on both sides.
\frac{AB^2}{AC^2} + \frac{BC^2}{AC^2} = \frac{AC^2}{AC^2}
\left(\frac{AB}{AC}\right)^2 + \left(\frac{BC}{AC}\right)^2 = \left(\frac{AC}{AC}\right)^2
(\sin \theta)^2 + (\cos \theta)^2 = 1^2 [using equation (I) and (II)]
\sin^2 \theta + \cos^2 \theta = 1
Hence, the identity is \sin^2 \theta + \cos^2 \theta = 1.
1 + \tan^2 \theta = \sec^2 \theta
Consider a right triangle ABC with angle \theta.
\tan \theta = \frac{AB}{BC} - - - - - (III)
\sec \theta = \frac{AC}{BC} - - - - - (IV)

By Pythagoras theorem:
AB^2 + BC^2 = AC^2
Divide by BC^2 on both sides.
\frac{AB^2}{BC^2} + \frac{BC^2}{BC^2} = \frac{AC^2}{BC^2}
\left(\frac{AB}{BC}\right)^2 + \left(\frac{BC}{BC}\right)^2 = \left(\frac{AC}{BC}\right)^2
(\tan \theta)^2 + 1^2 = (\sec \theta)^2 [using equation (III) and (IV)]
\tan^2 \theta + 1 = \sec^2 \theta
Hence, the identity is 1 + \tan^2 \theta = \sec^2 \theta.
1 + \cot^2 \theta = \text{cosec}^2\: \theta
Consider a right triangle ABC with angle \theta.
\cot \theta = \frac{BC}{AB} - - - - - (III)
\text{cosec}\: \theta = \frac{AC}{AB} - - - - - (IV)

By Pythagoras theorem:
AB^2 + BC^2 = AC^2
Divide by AB^2 on both sides.
\frac{AB^2}{AB^2} + \frac{BC^2}{AB^2} = \frac{AC^2}{AB^2}
\left(\frac{AB}{AB}\right)^2 + \left(\frac{BC}{AB}\right)^2 = \left(\frac{AC}{AB}\right)^2
1^2 + (\cot \theta)^2 = (\text{cosec}\: \theta)^2 [using equation (III) and (IV)]
1 + \cot^2 \theta + 1 = \text{cosec}^2\: \theta
Hence, the identity is 1 + \cot^2 \theta + 1 = \text{cosec}^2\: \theta.
Equal forms of trigonometric identities
Identity | Equal form of identity |
| \sin^2 \theta + \cos^2 \theta = 1 | \sin^2 \theta = 1 - \cos^2 \theta (or) \cos^2 \theta = 1 - \sin^2 \theta |
| 1 + \tan^2 \theta = \sec^2 \theta | \tan^2 \theta = \sec^2 \theta - 1 (or) \sec^2 \theta - \tan^2 \theta = 1 |
| 1 + \cot^2 \theta = \text{cosec}^2\: \theta | \cot^2 \theta = \text{cosec}^2\: \theta - 1 (or) \text{cosec}^2\: \theta - \cot^2 \theta = 1 |
Important!
The three trigonometric identities are true for every \theta lies between 0^\circ and 90^\circ.
