UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreBasic proportionality theorem or Thales theorem
Theorem 1: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
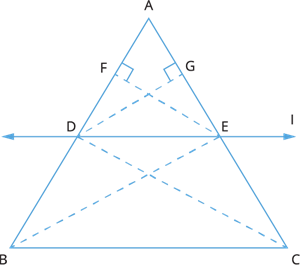
Given: In a triangle \(ABC\), a straight line \(l\) parallel to \(BC\) intersects \(AB\) at \(D\) and \(AC\) at \(E\).
To prove: \(\frac{AD}{DB} = \frac{AE}{EC}\)
Construction: Join \(BE\) and \(CD\). Draw \(EF \perp AB\) and \(DG \perp CA\).
Proof: Since \(EF \perp AB\), \(EF\) is the height of \(\triangle ADE\) and \(\triangle DBE\).
\(ar(\triangle ADE) = \frac{1}{2} \times AD \times EF\) and
\(ar(\triangle DBE) = \frac{1}{2} \times DB \times EF\)
Therefore, \(\frac{ar(\triangle ADE)}{ar(\triangle DBE)} = \frac{\frac{1}{2} \times AD \times EF}{\frac{1}{2} \times DB \times EF} = \frac{AD}{DB}\) ---- (\(1\))
Similarly, \(ar(\triangle ADE) = \frac{1}{2} \times AE \times DG\) and
\(ar(\triangle DCE) = \frac{1}{2} \times EC \times DG\)
Thus, \(\frac{ar(\triangle ADE)}{ar(\triangle DCE)} = \frac{\frac{1}{2} \times AE \times DG}{\frac{1}{2} \times EC \times DG} = \frac{AE}{EC}\) ---- (\(2\))
But, \(\triangle DBE\) and \(\triangle DCE\) are on the same base and between the same parallels \(BC\) and \(DE\).
Therefore, \(ar(\triangle DBE) = ar(\triangle DCE)\) ---- (\(3\))
From (\(1\)), (\(2\)) and (\(3\)), we have:
\(\frac{AD}{DB} = \frac{AE}{EC}\)
Hence, we proved.
Now, we shall learn the Converse of Basic proportionality theorem or Converse of Thales theorem.
Theorem 2: If a line divides any two sides of a triangle in the same ratio, then the line is parallel
to the third side.
to the third side.
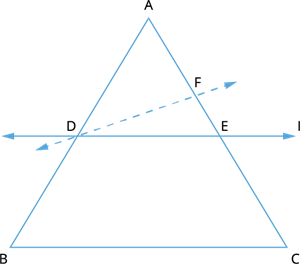
Given: A line \(l\) intersects the sides \(AB\) and \(AC\) of \(\triangle ABC\) at \(D\) and \(E\), respectively, such that \(\frac{AD}{DB} = \frac{AE}{EC}\) ---- (\(1\))
To prove: \(DE \parallel BC\)
Construction: If \(DE\) is not parallel to \(BC\), then draw a line \(DF \parallel BC\).
Proof: Since \(DF \parallel BC\), by Thales theorem, we get:
\(\frac{AD}{DB} = \frac{AF}{FC}\) ---- (\(2\))
From (\(1\)) and (\(2\)), we have:
\(\frac{AF}{FC} = \frac{AE}{EC}\)
Add \(1\) to both sides of the equation, we have:
\(\frac{AF}{FC} + 1 = \frac{AE}{EC} + 1\)
\(\frac{AF + FC}{FC} = \frac{AE + EC}{EC}\)
\(\frac{AC}{FC} = \frac{AC}{EC}\)
\(FC = EC\)
This is true only if \(F\) and \(E\) coincide.
Therefore, \(DE \parallel BC\)
Hence, we proved.
Register for free to see more content