Angles on a straight line, intersecting lines — lesson. Mathematics CBSE, Class 7.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

Straight lines:

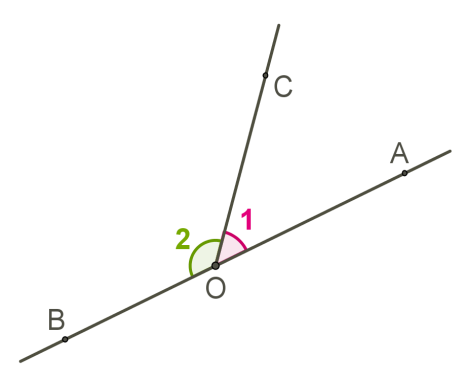
The angle

∡ AOB = 180 °

is a wide-angle, and a beam \(OC\) divides it into two parts then

∡ 1 + ∡ 2 = 180 °

The sum of two angles on a straight line is 180°, such angles are called Supplementary angles.

When two angles are supplementary, each angle is said to be the supplement of the other.

Example:

∠AOB and ∠BOC - adjacent angles

∠AOB + ∠BOC = ∠AOC .

∠AOC and ∠COP- linear pair.

Therefore, their sum is 180° (∠AOC + ∠COP = 180°).

Combining these two results we get ∠AOB + ∠BOC + ∠COP = 180°.

Thus, the sum of all the angles formed at a point on a straight line is 180°.

Intersecting lines:

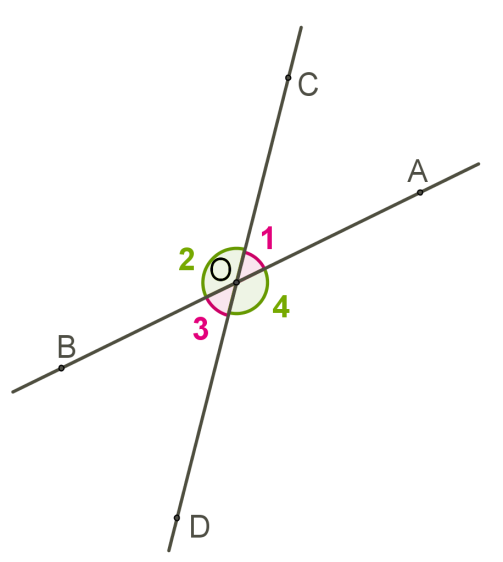
If two lines intersect, then two pairs of vertical angles are formed

∡ 1, ∡ 3

and

∡ 2, ∡ 4

∡ 1 + ∡ 2 = 180 °

and

∡ 1 + ∡ 4 = 180 °

by the property of adjacent angles, therefore,

∡ 2 = ∡ 4

It is also clear that

∡ 1 = ∡ 3

Vertical angles are equal.

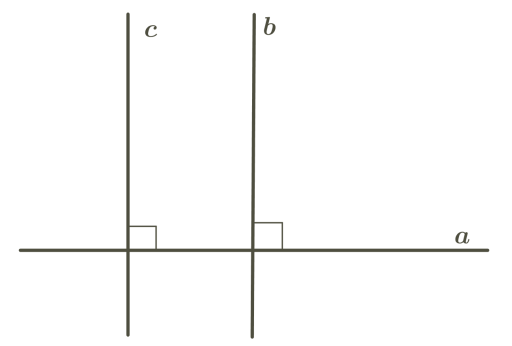
Perpendicular lines and angles formed by them

If one of the vertical angles of the line is equal to

90 °

, then the remaining angles are also straight.

If two intersecting straight lines form four right angles, they are called perpendicular.

It has written down

a ⊥ b

Two straight lines, perpendicular to the third, do not intersect.

Did you find an error?

1. Angles on a straight line, intersecting lines