UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreThe perimeter of a rectangle: The perimeter is the total distance around the outside, which can be constructed by adding together the length and breadth of each side.
Let us consider a rectangle \(ABCD\) of length \(l\) units and breadth \(b\) units. Therefore, the perimeter of the rectangle is as follows:
\(Perimeter (P) = (AB + BC + CD + DA)\) units.
\(P = ( l + b + l + b )\) units.
\(P = (2l + 2b)\) units.
\(P = 2 (l + b)\) units.
Thus, the length of perimeter \(l = P/2 - b\) unit.
And, the breadth of perimeter \(b = P/2 - l\) unit.
Area of rectangle: The area of a rectangle is given by multiplying the width times the height.
Let us consider a rectangle \(ABCD\) of length \(l\) units and breadth \(b\) units. Therefore, the area of the rectangle is as follows:
\(Area (A) = length × breadth\)
\(A = l × b\) square units.
Thus, the length of the rectangle \(l = A/b\) unit.
And, the breadth of the rectangle \(b = A/l\) unit.
Diagonals of rectangle: A rectangle has two diagonals they are equal in length and intersect in the middle. The diagonal is the square root of (width squared + height squared).
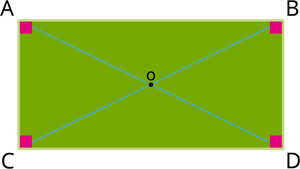
\(Diagonal (d) =\)
Where \(l\) is the length of the rectangle.
Where \( b\) is the breadth of the rectangle.
Register for free to see more content