Numerator less than denominator — lesson. Mathematics CBSE, Class 7.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

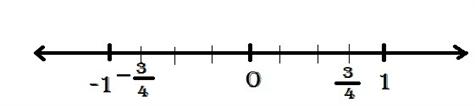
Book Free Demo

Let us consider

$\frac{3}{4}$ and

$- \frac{3}{4}$ . First, let us plot

$\frac{3}{4}$ .

Here, the numerator $3$ is less than the denominator $4$ .
Then the positive rational number will be between $0$ and $1$ .
Now, let us draw a number line and plot $1$ and $-1$ .
Then the number $\frac{3}{4}$ has to lie somewhere between $0$ and $1$ .
Now we divide the length between $0$ and $1$ into equal parts.
The Denominator gives us the number of equal parts( $4$ ).
It is $4$ , so we divide it into $4$ equal parts.

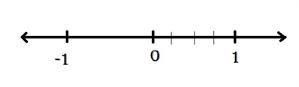
The numerator tells us the number of parts starting from zero.
Here, it is $3$ . So we mark the point $3$ parts away from the zero as shown in the below figure.

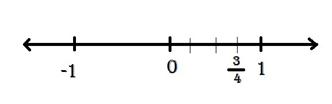
num22 - Copy.jpg

Similarly,

$- \frac{3}{4}$ can be marked using the same procedure because

$- \frac{3}{4}$ is the corresponding value of

$\frac{3}{4}$ .

We know that it lies between $0$ and $-1$ . So, we divide it into four equal parts and mark $3$ parts away from the zero, as shown in the below figure.

num22 - Copy - Copy.jpg

Previous theory

Exit to the topic

Did you find an error?

Register for free to see more content

Register for free to see more content