Altitude of different types of triangle. — lesson. Mathematics CBSE, Class 7.

PDF chapter test TRY NOW

Altitude position differs for various types of triangle. Let us discuss its types:

Acute angled triangle

Right angled triangle

Obtuse angled triangle

Equilateral triangle and

Isosceles triangle

Altitude in acute angled triangle:

All three altitude lies inside the triangle.

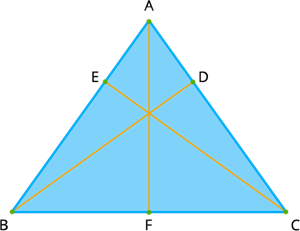
Here

$ABC$ is an acute-angled triangle and

$AF, BD$ and

$CE$ are the altitudes of the triangle

$ABC$ and all three altitudes lies inside the triangle.

Altitude in right angled triangle:

The altitude perpendicular to the hypotenuse lies inside the triangle, but the other two altitudes are the legs of the triangle.

Here

$ABC$ is a right-angled triangle, and

$BD$ is the altitude perpendicular to the hypotenuse lies inside the triangle, but the other two altitudes

$AB$ and

$BC$ are the legs of the triangle.

Altitude in obtuse angled triangle:

The altitude connected to the obtuse vertex lies inside the triangle, but the two altitudes connected to the acute vertices are outside the triangle.

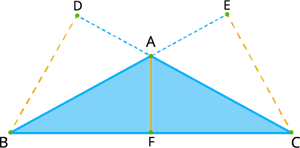
Here

$ABC$ is an obtuse-angled triangle, and

$AF$ is the altitude connected to the obtuse vertex lies inside the triangle, but the other two altitudes

$BD$ and

$CE$ connected to the acute vertices are outside the triangle.

Altitude in equilateral triangle:

The altitudes of an equilateral triangle bisect its base and the opposite angle.

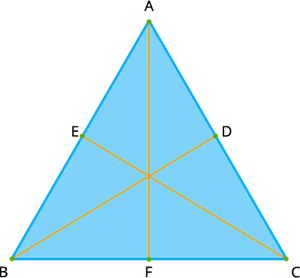
Here

$ABC$ is an equilateral triangle and

$AF, BD$ and

$CE$ are the altitudes lie inside the triangle as it an acute-angled triangle. Also, altitudes of an equilateral triangle bisect its base and the opposite angle. For an equilateral triangle, the all three lines

$AF, BD$ and

$CE$ are altitudes, medians as well as angle bisector of the triangle

$ABC$ .

Altitude in isosceles angled triangle:

The altitudes of an isosceles triangle bisect its unequal base and the opposite angle. But this will not suit for other

$2$ altitudes.

Here

$ABC$ is an isosceles triangle and

$AF, BD$ and

$CE$ are the altitudes of the triangle. Also, altitudes of an isosceles triangle bisect its unequal base

$BC$ and the opposite angle

$A$ , but this will not be true for the equal bases

$AC$ and

$AB$ and the opposite angles

$B$ and

$C$ .

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

2. Altitude of different types of triangle.

Theory: