UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreIn any triangle, the difference in the length of any two sides of a triangle is always lesser than the third side.
In here, the inequalities are as follows:
\(a - b < c\)
\(b - c < a\) and
\(c - a < b\)
Example:
Consider the triangle\(ABC\) whose sides measures are \(AB = c = 3 cm, BC = a = 4 cm\) and \(AC = b =5 cm\).
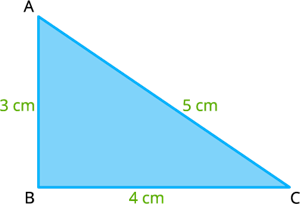
Let's check the triangle inequality for the triangle \(ABC\),
\(a - b = 4 - 5 = -1 < 3 = c\)
\(b - c = 5 - 3 = 2 < 4 = a\) and
\(c - a = 3 - 4 = -1 < 5 = b\)
Important!
Suppose \(a, b\) and \(c\) are the sides of a triangle with \(a\) and \(b\) are known sides and \(c\) is unknown. Let's use the triangle inequality to find the third side \(c\). As the sum of two sides\((a+b)\) of a triangle is always greater than the third side\((c)\), and difference of two sides\((a-b)\) of a triangle is always lesser than the third side\((c)\), the length of the third side\((c)\) must lie between difference\((a-b)\) and sum\((a+b)\).
Register for free to see more content