Cube root — lesson. Mathematics CBSE, Class 8.

PDF chapter test TRY NOW

The inverse operation of a cube is cube root. The symbol used to represent the cube root is

$\sqrt[3]{}$ .

A cube root is a unique value that gives us the original number when we multiply itself by three times.

The cube root of

$a$ is denoted by

$\sqrt[3]{a}$ or

$a^{\frac{1}{3}}$ .

Example:

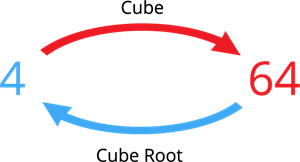
Find the cube root of

$64$ .

Solution:

$\sqrt[3]{64} = \sqrt[3]{4 \times 4 \times 4}$

$= \sqrt[3]{4^3}$

$= 4$

Therefore, the cube root of

$64$ is

$4$ .

By the observation of the above example, we can conclude that:

The cube of

$4$ is

$64$ .

The cube root of

$64$ is

$4$ .

cube_4_64 (1).png

The following table consist of cube and cube roots of the first

$20$ numbers.

Number	Cube number	Cube root	Number	Cube number	Cube root
1	$1^3 = 1$	$\sqrt[3]{1} = 1$	11	$11^3 = 1331$	$\sqrt[3]{1331} = 11$
2	$2^3 = 8$	$\sqrt[3]{8} = 2$	12	$12^3 = 1728$	$\sqrt[3]{1728} = 12$
3	$3^3 = 27$	$\sqrt[3]{27} = 3$	13	$13^3 = 2197$	$\sqrt[3]{2197} = 13$
4	$4^3 = 64$	$\sqrt[3]{64} = 4$	14	$14^3 = 2744$	$\sqrt[3]{2744} = 14$
5	$5^3 = 125$	$\sqrt[3]{125} = 5$	15	$15^3 = 3375$	$\sqrt[3]{3375} = 15$
6	$6^3 = 216$	$\sqrt[3]{216} = 6$	16	$16^3 = 4096$	$\sqrt[3]{4096} = 16$
7	$7^3 = 343$	$\sqrt[3]{343} = 7$	17	$17^3 = 4913$	$\sqrt[3]{4913} = 17$
8	$8^3 = 512$	$\sqrt[3]{512} = 8$	18	$18^3 = 5832$	$\sqrt[3]{5832} = 18$
9	$9^3 = 729$	$\sqrt[3]{729} = 9$	19	$19^3 = 6859$	$\sqrt[3]{6859} = 19$
10	$10^3 = 1000$	$\sqrt[3]{1000} = 10$	20	$20^3 = 8000$	$\sqrt[3]{8000} = 20$

Exit to the topic

Did you find an error?

Register for free to see more content

Register for free to see more content