UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
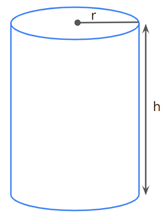
Learn moreA cylinder has two plane ends. Each plane end is circular, and these two plane ends are parallel to each other.
Also, a cylinder has two dimensions, namely radius and height.
The net of a cylinder looks like this.
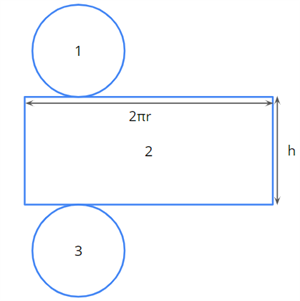
\(\text{The total surface area of a cylinder}\) \(=\) \(\text{Area}\) \(1\) \(+\) \(\text{Area}\) \(2\) \(+\) \(\text{Area}\) \(3\)
\(= \pi r^2 + 2\pi rh + \pi r^2\)
[Since \(\text{Area}\) \(1\) and \(\text{Area}\) \(3\) are circles]
\(= 2\pi r^2 + 2\pi rh\)
\(= 2\pi r(r + h)\)
Let us now look at the lateral surface of the cylinder.
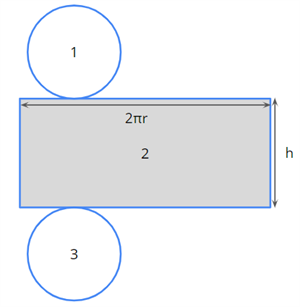
The shaded portion forms the lateral surface of the cylinder.
\(\text{The lateral (or curved) surface area of a cylinder}\) \(=\) \(\text{Area}\) \(2\) \(=\) \(2\pi rh\)
Register for free to see more content