PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet's us find the sum of the interior angles of any polygon.
We can extend the angle sum property theorem to any polygons by splitting the polygons into triangles.
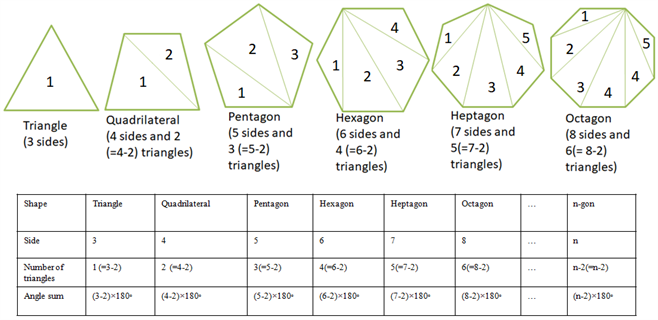
From the above table, it is clear that for any polygon with \(n\) sides the sum of the interior angle is \((n-2)\)\(×180°\).
Thus, the sum of the interior angle of a polygon is \((n-2)×180°\).
Let us find each interior angle of a regular polygon:
We know that 'a regular polygon is a polygon whose all sides and all angles are equal. Thus, a regular polygon is both equiangular and equilateral'.
As all the angles are equal in a regular polygon, each interior angle of a polygon is degree.
- The sum of all interior angles of a polygon with '\(n\)' sides is \((n-2)×180°\).
- Each interior angle of a regular polygon with '\(n\)' sides is .
Important!
Register for free to see more content