UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn more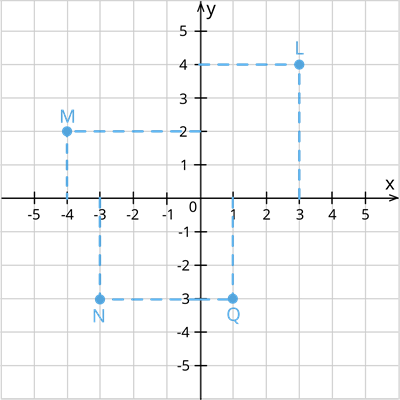
1. The perpendicular distance of the point \(L\) from the \(y\) - axis measured along the positive direction of the \(y\)-axis is \(LX = 4\) units. The perpendicular distance of the point \(L\) from the \(x\)-axis measured along the positive direction of the \(x\)- axis \(OL = 3\) units.
Point L lies in first quadrant in the above graph. Hence its co-ordinates will be represented as (x, y), where \(x = 3\) and \(y = 4\) the co-ordinate of \(L\) in cartesian plane is \((3,4)\).
2. The perpendicular distance of the point \(M\) from the \(y\) - axis measured along the positive direction of the \(y\)-axis is \(MX' = 2\) units. The perpendicular distance of the point \(M\) from the x-axis measured along the negative direction of the \(x\) - axis \(OM = 2\) units.
Point M lies in second quadrant in the above graph. Hence its co-ordinates will be represented as (-x, y), where \(x = 4\) and \(y = 2\) the co-ordinate of M in cartesian plane is \((-4,2)\).
3. The perpendicular distance of the point \(N\) from the \(y\) - axis measured along the negative direction of the \(y\)-axis is \(NX' = 3\) units. The perpendicular distance of the point \(N\) from the \(x\)-axis measured along the negative direction of the \(x\) - axis \(OX' = 2\) units.
Point N lies in third quadrant in the above graph. Hence its co-ordinates will be represented as (-x, -y), where \(x = 2\) and \(y = 3\) the co-ordinate of \(L\) in cartesian plane is \((-2,-3)\).
4. The perpendicular distance of the point \(Q\) from the \(y\) - axis measured along the negative direction of the y-axis is \(QX' = 3\) units. The perpendicular distance of the point \(Q\) from the \(x\)-axis measured along the positive direction of the \(x\) - axis \(OX = 1\) unit.
Point \(Q\) lies in fourth quadrant in the above graph. Hence its co-ordinates will be represented as (x, -y), where \(x = 1\) and \(y = 3\) the co-ordinate of \(L\) in cartesian plane is \((1,-3)\).
Register for free to see more content