52. Exemplar exercise problems XVII

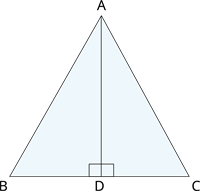
$ABC$ is an isosceles triangle with $AB = AC$ and $D$ is a point on $BC$ such that $AD \perp BC$. To prove that $\angle BAD = \angle CAD$, a student proceeded as follows:

 

In $\triangle ABD$ and $\triangle ACD$,

 

$AB = AC$ [Given]

 

$\angle B = \angle C$ [because $AB = AC$]

 

and $\angle ADB = \angle ADC$

 

Therefore, $\triangle ABD \cong \triangle ACD$ [AAS]

 

So, $\angle BAD = \angle CAD$ [CPCT]

 

What is the defect in the above arguments?

 

 

[Hint: Recall how $\angle B = \angle C$ is proved when $AB = AC$].