Exercise Problem XVII — task. Mathematics CBSE, Class 9.

PDF chapter test TRY NOW

$∆ ABC$ and

$∆ DBC$ are two isosceles triangles on the same base

$BC$ and vertices

$A$ and

$D$ are on the same side of

$BC$ (see Fig. 7.39).

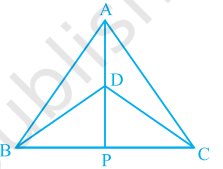
$AD$ is extended to intersect

$BC$ at

$P$ , show that

(i)

$∆ ABD ≅ ∆ ACD$

(ii)

$∆ ABP≅ ∆ ACP$

(iii)

$AP$ bisects

$∠ A$ as well as

$∠ D$ .

(iv)

$AP$ is the perpendicular bisector of

$BC$ .

You cannot attach a file at the moment. This functionality is under development, exercise is for information only.

Important!

This is a creative exercise. Your teacher will check it manually.

Did you find an error?

25. Exercise Problem XVII