UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreLet us learn how to graphically solve \(2\) quadratic equations.
Example:
1. Draw the graph of \(y = x^2 + 2x - 3\) and hence solve \(x^2 - x - 6 = 0\).
Solution:
Step 1: Draw the graph of the equation \(y = x^2 + 2x - 3\).
The table of values for the equation \(y = x^2 + 2x - 3\) is given by:
| \(x\) | \(-4\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(y\) | \(5\) | \(0\) | \(-3\) | \(-4\) | \(-3\) | \(1\) | \(5\) |
Step 2: To solve the equation \(x^2 - x - 6 = 0\), subtract the equation \(x^2 - x - 6 = 0\) from \(y = x^2 + 2x - 3\).
\(y = x^2 + 2x - 3\)
\(0 = x^2 - x - 6\) (\(-\))
-----------------------------
\(y = x + 3\)
-----------------------------
Step 3: Draw the graph of the equation \(y = x + 3\).
The table of values for the equation \(y = x + 3\) is given by:
| \(x\) | \(-4\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
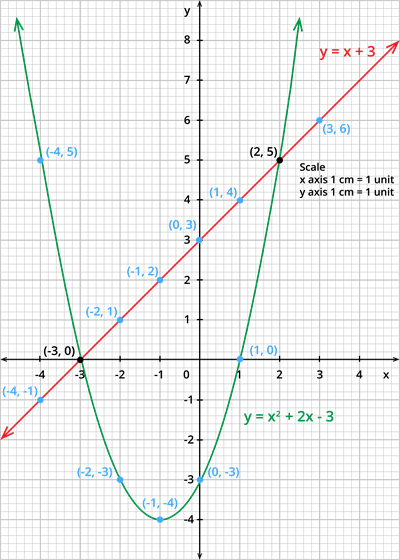
Step 4: Mark the points of intersection of \(y = x^2 + 2x - 3\) and \(y = x + 3\). The point of intersection is \((-3,0)\) and \((2,5)\).
Step 5: The \(x\) - coordinates of the points are \(-3\) and \(2\). Therefore, the solution set for the equation \(x^2 - x - 6 = 0\) is \({-3,2}\).
2. Draw the graph of \(y = 2x^2 + x - 2\) and hence solve \(2x^2 = 0\).
Step 1: Draw the graph of the equation \(y = 2x^2 + x - 2\).
The table of values for the equation \(y = 2x^2 + x - 2\) is given by:
| \(x\) | \(-2\) | \(0\) | \(2\) |
| \(y\) | \(4\) | \(-2\) | \(8\) |
Step 2: To solve the equation \(2x^2 = 0\), subtract \(2x^2 = 0\) from \(y = 2x^2 + x - 2\).
\(y = 2x^2 + x - 2\)
\(0 = 2x^2\) (\(-\))
-------------------------------
\(y = x - 2\)
-------------------------------
Step 3: Draw the graph of the equation \(y = x - 2\).
The table of values for the equation \(y = x - 2\) is given by:
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y\) | \(-4\) | \(-3\) | \(2\) | \(-1\) | \(0\) | \(1\) |
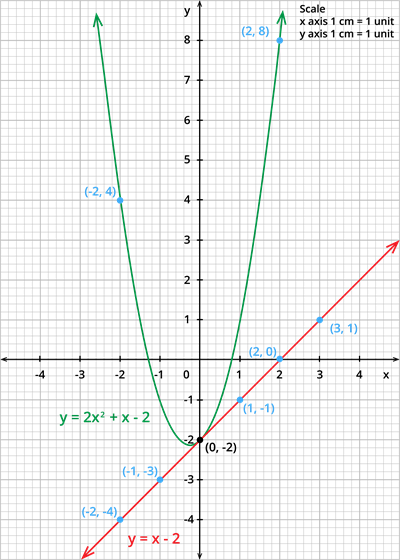
Step 4: Mark the points of intersection of \(y = 2x^2 + x - 2\) and \(y = x - 2\). The point of intersection is \((0,-2)\).
Step 5: The \(x\) - coordinates of the points is \(0\). Therefore, the solution set for the equation \(2x^2 = 0\) is \(0\).
Register for free to see more content