PDF chapter test TRY NOW
Let us find the equation of the straight line whose intercepts are \(a\) and \(b\) on the coordinate axes, respectively.
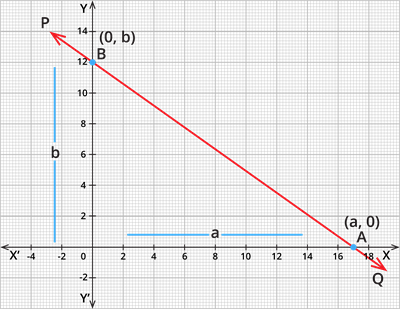
Let \(PQ\) be a straight line that meets the \(x\) - axis at the point \(A\) and the \(y\) axis at the point \(B\). The coordinates of points \(A\) and \(B\) are \((a,0)\) and \((0,b)\), respectively. Then, \(OA = a\) and \(OB = b\).
Here, \((x_1,y_1) = (a,0)\) and \((x_2,y_2) = (0,b)\).
Substituting the known values in two point form equation, we get:
\(\frac{y - 0}{b - 0} = \frac{x - a}{0 - a}\)
\(\frac{y}{b} = \frac{x - a}{-a}\)
\(\frac{y}{b} = \frac{-x}{a} + 1\)
\(\frac{x}{a} + \frac{y}{b} = 1\)
Hence, the equation of the intercept of the line is \(\frac{x}{a} + \frac{y}{b} = 1\).
Example:
Find the intercepts of the line \(-3x + 4y + 12 = 0\) on the coordinate axes.
Solution:
The given equation is \(-3x + 4y + 12 = 0\).
Let us write the equation in the normal form.
\(-3x + 4y = -12\)
\(\frac{-3}{-12}x + \frac{4}{-12}y = \frac{-12}{-12}\) [Dividing by \(-12\) on both sides so that the RHS is equal to \(1\)]
\(\frac{x}{4} + \frac{y}{-3} = 1\)
Comparing the above equation with the equation of the intercept of the line \(\frac{x}{a} + \frac{y}{b} = 1\), we get:
\(a = 4\) and \(b = -3\)
Therefore, the intercept of the line is \(a = 4\) and \(b = -3\).
Register for free to see more content