Construction of similar triangles — lesson. Mathematics State Board, Class 10.

UPSKILL MATH PLUS

Learn Mathematics through our AI based learning portal with the support of our Academic Experts!

A scale factor is the ratio of similar figures' corresponding sides.

In the above theoretical material, we deal with similar triangles theoretically. Let us discuss how to construct a similar triangle using the concept of the scale factor. There are

$2$ cases.

Let us understand the cases using examples.

Example:

Case 1: If the scale factor is less than

$1$ .

Construct a triangle similar to the given triangle

$PQR$ with its sides equal to

$\frac{2}{5}$ of the corresponding sides of the triangle

$PQR$ .

Solution:

Given a triangle

$PQR$ . We are required to construct another triangle whose sides are

$\frac{2}{5}$ of the corresponding sides of the triangle

$PQR$ .

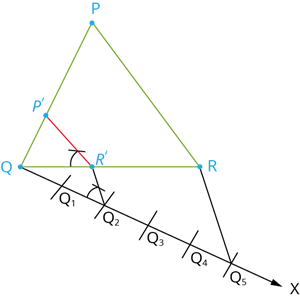
Construction:

Step 1: Construct a triangle

$PQR$ with any measurement.

Step 2: Draw a ray

$QX$ making an acute angle with

$QR$ on the side opposite to vertex

$P$ .

Step 3: Locate

$5$ (the greater of

$2$ and

$5$ in

$\frac{2}{5}$ ) points.

$Q_1$ ,

$Q_2$ ,

$Q_3$ ,

$Q_4$ and

$Q_5$ on

$QX$ so that

$QQ_1 = Q_1Q_2 = Q_2Q_3 = Q_3Q_4 = Q_4Q_5$ .

Step 4: Join

$Q_5R$ and draw a line through

$Q_2$ (the second point,

$2$ being smaller of

$2$ and

$5$ in

$\frac{2}{5}$ ) parallel to

$Q_5R$ to intersect

$QR$ at

$R'$ .

Step 5: Draw a line through

$R'$ parallel to the line

$RP$ to intersect

$QP$ at

$P'$ . Then,

$P'QR'$ is the required triangle, each of whose side is two - fifths of the corresponding sides of

$\triangle PQR$ .

Let us consider the construction of triangle

$ABC$ using the scale factor

$\frac{3}{4}$ .

Case 2: If the scale factor is greater than

$1$ .

Construct a triangle similar to a given triangle

$PQR$ with its sides equal to

$\frac{3}{2}$ of the corresponding sides of the triangle

$PQR$ .

Solution:

Given a triangle

$PQR$ . We are required to construct an another triangle whose sides are

$\frac{3}{2}$ of the corresponding sides of the triangle

$PQR$ .

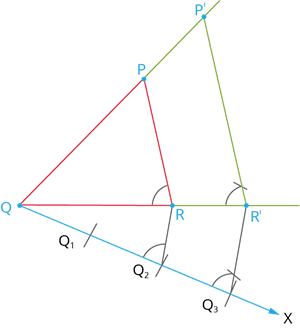
Construction:

Step 1: Construct a triangle

$PQR$ with any measurement.

Step 2: Draw a ray

$QX$ making an acute angle with

$QR$ on the side opposite to vertex

$P$ .

Step 3: Locate

$3$ (the greater of

$2$ and

$3$ in

$\frac{3}{2}$ ) points.

$Q_1$ ,

$Q_2$ , and

$Q_3$ on

$QX$ so that

$QQ_1 = Q_1Q_2 = Q_2Q_3$ .

Step 4: Join

$Q_2$ (the 2nd point, 2 being smaller of

$2$ and

$3$ in

$\frac{3}{2}$ ) to

$R$ and draw a line through

$Q_3$ parallel to

$Q_2R$ , intersecting the extended line segment

$QR$ at

$R'$ .

Step 5: Draw a line through

$R'$ parallel to the line

$RP$ intersecting the extended line segment

$QP$ at

$P'$ . Then,

$P'QR'$ is the required triangle, each of whose side is three - twos of the corresponding sides of

$\triangle PQR$ .

Let us consider the construction of triangle

$ABC$ using the scale factor

$\frac{5}{3}$ .

Previous theory

Exit to the topic

Next exercise

Send feedback

Did you find an error?

Send it to us!

6. Construction of similar triangles

Theory: