PDF chapter test TRY NOW

7. Construction of a triangle if its base, vertical angle and the point on the base are given

Learn how to construct a triangle with an example if its base, vertical angle and the point on the base where the bisector of the vertical angle meets the base are given.

Example:

Draw a triangle

$ABC$ of base

$AB = 7 \ cm$ ,

$\angle C = 30^{\circ}$ and the bisector of

$\angle C$ meets

$AB$ at

$C$ such that

$AD = 5 \ cm$ .

Solution:

First, let us draw a rough figure.

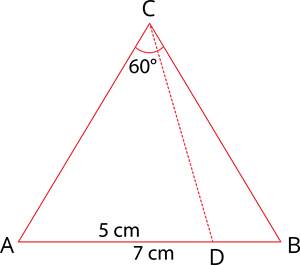
Construction:

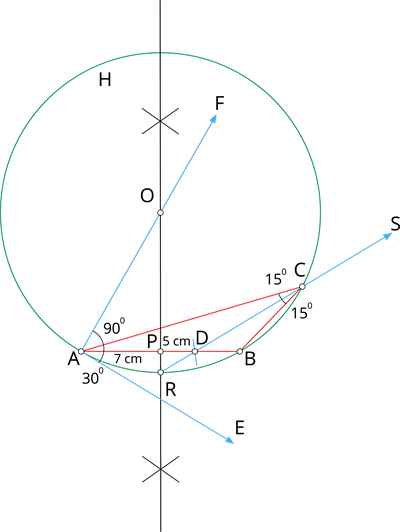
Step 1: Draw a line segment

$AB = 7 \ cm$ .

Step 2: At

$A$ , draw

$AE$ such that

$\angle EAB = 30^{\circ}$ .

Step 3: At

$A$ , draw

$AF$ such that

$\angle FAE = 90^{\circ}$ .

Step 4: Draw the perpendicular bisector to

$AB$ , which intersects

$AF$ at

$O$ and

$AB$ at

$P$ .

Step 5: Draw a circle with

$O$ as the centre and

$OA$ as the radius.

Step 6: From

$A$ , mark an arc of

$5 \ cm$ on

$AB$ at

$D$ .

Step 7: The perpendicular bisector intersects the circle at

$R$ . Join

$RD$ .

Step 8:

$RD$ produced meets the circle at

$C$ . Now, join

$AC$ and

$AB$ .

Thus,

$\triangle ABC$ is the required triangle.

Previous theory

Exit to the topic

Next exercise

Send feedback

Did you find an error?

Send it to us!

7. Construction of a triangle if its base, vertical angle and the point on the base are given

Theory: