UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
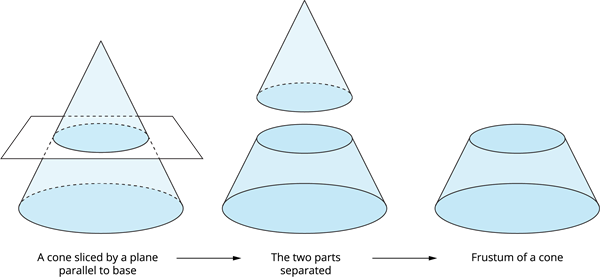
Learn moreFrustum of a cone:
If a smaller end of the cone is sliced by a plane parallel to its base, the portion of a solid between this plane and the base is known as the frustum of a cone.
Volume of a frustum of a cone:
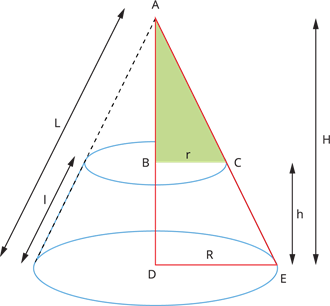
Let \(R\) and \(r\) be the radii of base \((R > r)\), \(h\) be the height, and \(l\) be the slant height of the frustum of a cone.
We need to find the height of the smaller cone \(ADE\).
Consider \(\Delta ABC\) and \(\Delta ADE\).
\(\angle BAC = \angle DAE\) [common angle]
\(\angle ABC = \angle ADE\) [Both \(90^\circ\)]
Therefore, \(\Delta ABC \sim \Delta ADE\) [by AA similarity].
The corresponding sides of similar triangles are proportional.
\(\frac{AB}{AD} = \frac{BC}{DE}\)
\(\frac{H - h}{H} = \frac{r}{R}\)
\(HR - hR = Hr\)
\(HR - Hr = hR\)
\(H(R - r) = hR\)
\(H = \frac{hR}{(R - r)}\) - - - - - - (I)
Volume of frustum \(=\) Volume of big cone \(-\) Volume of small cone
\(=\) Volume of \(ADE\) cone \(-\) Volume of \(ABC\) cone
\(=\) \(\frac{1}{3} \pi R^2H\) \(-\) \(\frac{1}{3} \pi r^2(H - h)\)
\(=\) \(\frac{1}{3} \pi R^2H\) \(-\) \(\frac{1}{3} \pi r^2H \) \(+\) \(\frac{1}{3} \pi r^2h\)
\(=\) \(\frac{1}{3} \pi H (R^2 - r^2)\) \(+\) \(\frac{1}{3} \pi r^2h\)
\(=\) \(\frac{1}{3} \pi \times \frac{hR}{(R - r)} (R^2 - r^2)\) \(+\) \(\frac{1}{3} \pi r^2h\) [using equation (I)]
\(=\) \(\frac{1}{3} \pi \times \frac{hR}{(R - r)} (R - r) (R + r)\) \(+\) \(\frac{1}{3} \pi r^2h\)
\(=\) \(\frac{1}{3} \pi hR(R + r)\) \(+\) \(\frac{1}{3} \pi r^2h\)
\(=\) \(\frac{1}{3} \pi h[R(R + r) + r^2]\)
\(=\) \(\frac{1}{3} \pi h[R^2 + Rr + r^2]\)
Volume of the frustum of a cone \(=\) \(\frac{1}{3} \pi h[R^2 + Rr + r^2]\) cu. units
Register for free to see more content