PDF chapter test TRY NOW
Definition:
If \(A\), \(B\) and \(C\) are three non-empty sets, then the cartesian product of three sets is the set of all possible ordered triplets given by \(A \times B \times C\) \(=\) \(\{(a, b, c) \text{ for all } a \in A, b \in B, c \in C\}\).
Illustration:
Let us consider the following example for the geometrical understanding of the cartesian product of two and three sets.
Consider three sets \(A\), \(B\) and \(C\).
Where \(A\) \(=\) \(\{2, 3\}\), \(B\) \(=\) \(\{2, 3\}\) and \(C\) \(=\) \(\{2, 3\}\).
First, let us find the product \(A \times B\).
\(A \times B\) \(=\) \(\{2, 3\} \times \{2, 3\}\)
\(A \times B\) \(=\) \(\{(2 ,2), (2, 3), (3, 2), (3, 3)\}\)
The product \(A \times B\) is geometrically represented as follows:
 |
Here, the product of two sets is represented in the \(xy\) \(-\) plane.
The product \(A \times B\) represents the vertices of a square in two dimensions.
Now let us find the product \(A \times B \times C\).
\(A \times B \times C\) \(=\) \((A \times B) \times C\).
\(A \times B \times C\) \(=\) \(\{(2 ,2), (2, 3), (3, 2), (3, 3)\}\) \(\times\) \(\{2, 3\}\).
\(A \times B \times C\) \(=\) \(\{(2 ,2, 2), (2 ,2, 3), (2, 3, 2), (2, 3, 3), (3, 2, 2), (3, 2, 3), (3, 3, 2), (3, 3, 3)\}\).
The product \(A \times B \times C\) is geometrically represented as follows:
 |
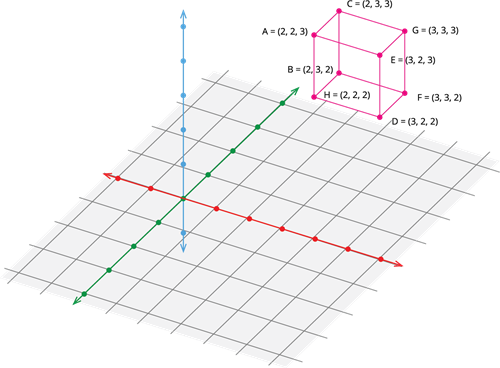Here, the product of three sets is represented in the \(xyz\) \(-\) plane.
The product \(A \times B \times C\) represents the vertices of a cube in three dimensions.
Important!
The cartesian product of two non-empty sets provides a shape in \(2\) \(-\) dimension, whereas the cartesian product of three non-empty sets provides a shape in \(3\) \(-\) dimension.
Register for free to see more content