
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoThe Lowest Common Multiple (LCM) of two or more given numbers is the smallest of their common multiples. It is also called the least common multiple.
To find the LCM of two or more numbers, we can use any of the following methods.
1. Common multiple method
2. Prime factorisation method
3. Division method
Common multiple method:
Find the lowest common multiple of the numbers 8 and 12.
Multiple of 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...
Multiple of 12 = 12, 24, 36, 48, 60, 72, 84, …
The common multiple of 8, 12 and 18 are 24, 48, 72, ...
The lowest common multiple of 8 and 12 is 24.
Prime factorisation method:
Find the LCM of 4, 8 and 12.
First, write each number as a product of its prime factors.
Next, select the common multiples of 4, 8 and 12.
Then, select the numbers which are left uncommon.
Finally, multiply all the selected numbers. You will get the lowest common multiple of those three numbers.
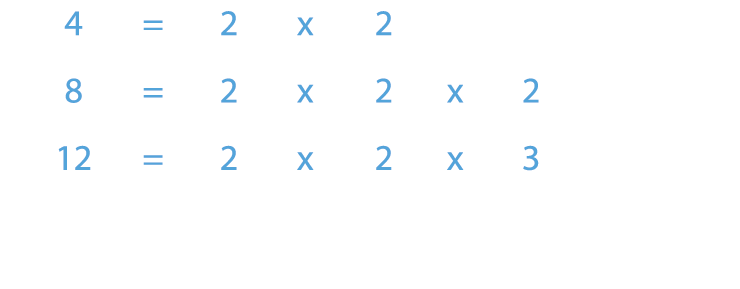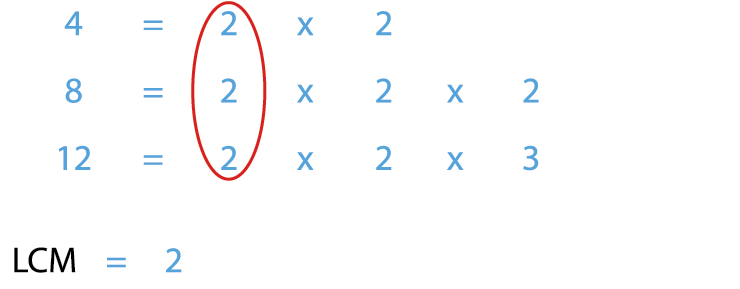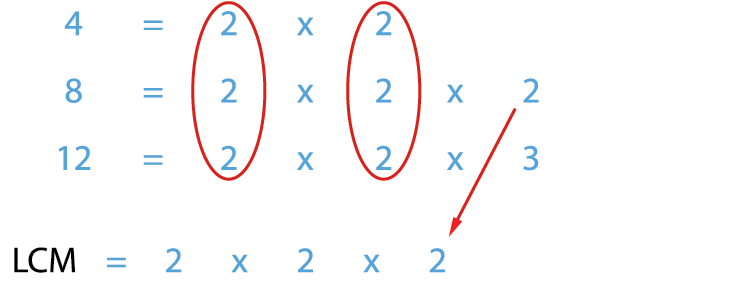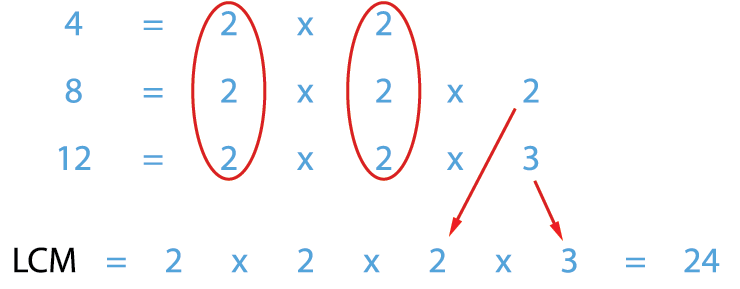
Therefore, LCM of 4, 8 and 12 = 24.
Division method:
The division method is a very convenient method of finding the LCM. We proceed as follows with this method of prime factorisation:
- Arrange all the given numbers in a row and separated by commas.
- Start with the lowest prime number which at least divides exactly one of the numbers.
- Write down the quotients and any undivided numbers in the next line.
- The only common factor is to repeat the process, as shown below to 1.
- Find the product of all the divisors. This is the required LCM.
Example:
Find the LCM of 8, 15 and 24.
Solution:
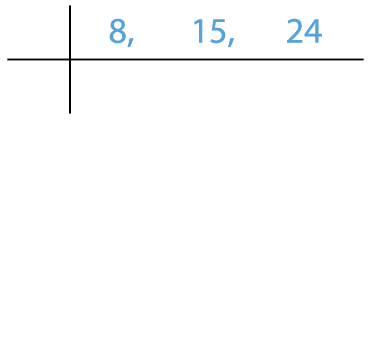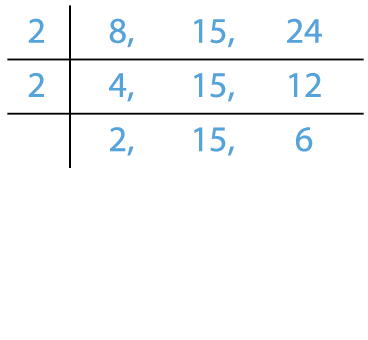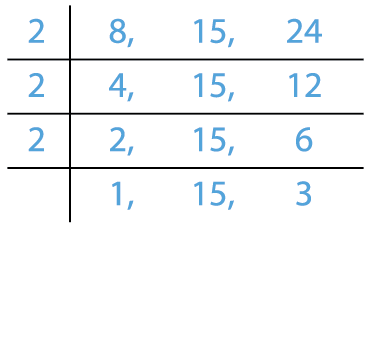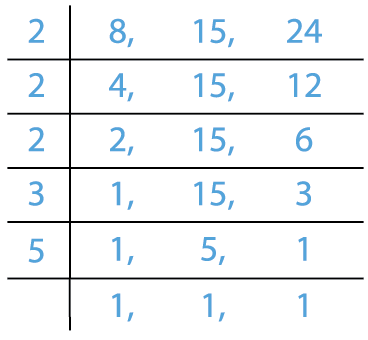
LCM = 2 \times 2 \times 2 \times 3 \times 5 = 120
Therefore, LCM of 8, 15 and 24 is 120.
The LCM is the product of both numbers when two numbers are co-prime.
Example:
Let us see the LCM of 7 and 13.
7 = 7×1 and 13=1×13
Both are co-prime numbers.
LCM is the product of both numbers.
7×13=91
LCM of 7 and 13 is 91.