PDF chapter test TRY NOW
Common factor
When we find factors for two or more numbers if any factors are common (same) between the numbers, they are called common factors.
Example:
1. Find the common factors of \(8\) and \(24\).
| \(1 \times 8 = 8\) | \(2 \times 4 = 8\) | \(4 \times 2 = 8\) |
We stop here because \(2\) and \(4\) already exist as a factor.
| \(1 \times 24 = 24\) | \(2 \times 12 = 24\) | \(3 \times 8 = 24\) | \(4 \times 6 = 24\) | \(6 \times 4 = 24\) |
We stop here because \(4\) and \(6\) already exist as a factor.
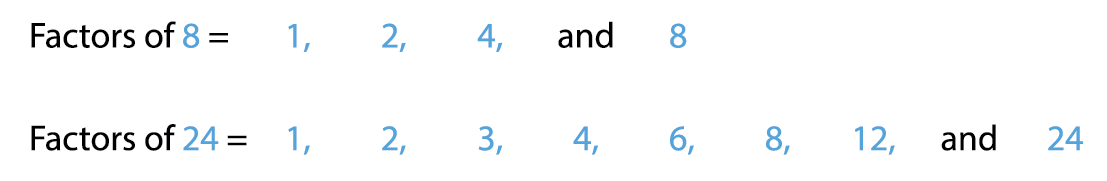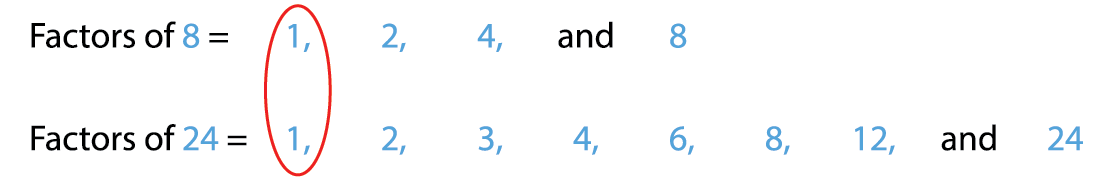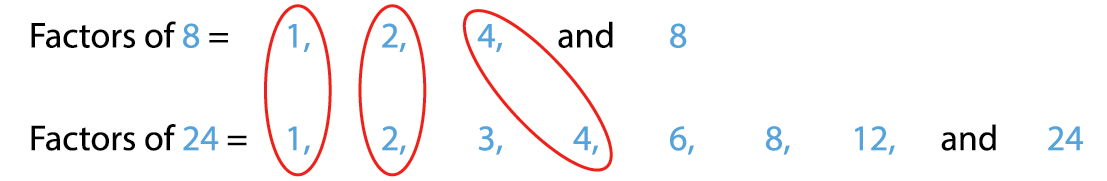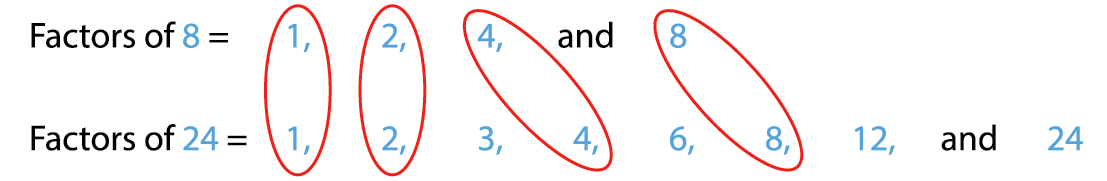
Common factors of \(8\) and \(24\) are \(1\), \(2\), \(4\) and \(8\).
2. Find common factors of \(15\), \(45\) and \(50\).
| \(1 \times 15 = 15\) | \(3 \times 5 = 15\) | \(5 \times 3 = 15\) |
We stop here because \(3\) and \(5\) already exist as a factor.
| \(1 \times 45 = 45\) | \(3 \times 15 = 45\) | \(5 \times 9 = 45\) | \(9 \times 5 = 45\) |
We stop here because \(5\) and \(9\) already exist as a factor.
| \(1 \times 50 = 50\) | \(2 \times 25 = 50\) | \(5 \times 10 = 50\) | \(10 \times 5 = 50\) |
We stop here because \(5\) and \(10\) already exist as a factor.
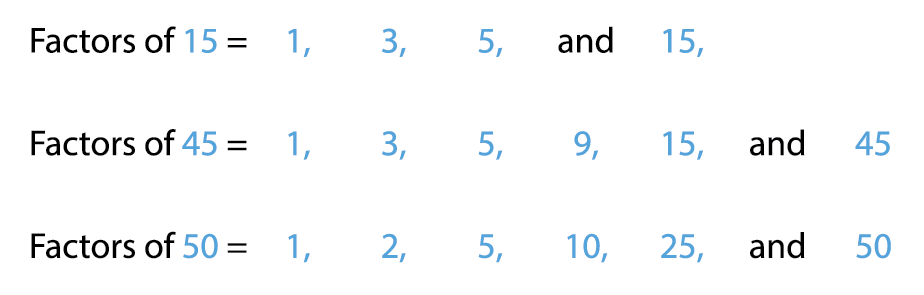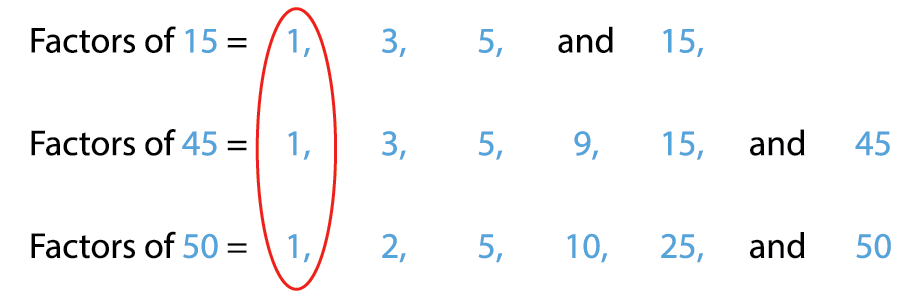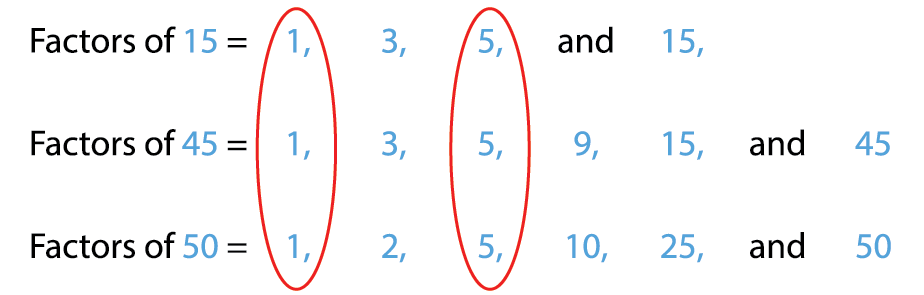
Common factors of \(15\), \(45\) and \(50\) are \(1\) and \(5\).
Register for free to see more content