UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreNow, we shall find the area of the right-angled triangle.
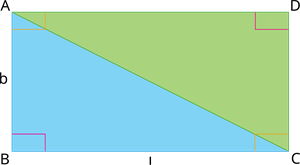
Let us consider a rectangle. When we cut a rectangle through the diagonal, we make \(2\) right-angled triangles.
In this right-angled triangle, the base of the angle containing \(90^{\circ}\) is considered as base (\(b\)) \(units\), and the other side is considered as height (\(h\)) \(units\).
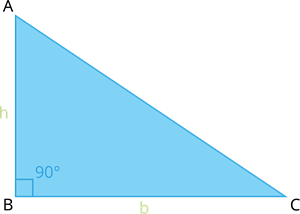
Then, the area of the right-angled triangle \(ABC\) is given by:
\(2\times \) Area of the right-angled triangle \(=\) Area of the rectangle
\(2\times \) Area of the right-angled triangle \(= l \times b\)
Area of the right-angled triangle \(=\frac{1}{2} (l \times b)\)
Here, the base and height of the right-angled triangle are the length and breadth of the rectangle, respectively.
Therefore, the area of the right-angled triangle is \(\frac{1}{2} (b \times h)\)\(sq. \ units\).
Example:
1. Let the base and height of the right-angled triangle be \(6 \ cm\) and \(10 \ cm\), respectively. Find the area of the right-angled triangle.
Solution:
Let \(b\) denote the base and \(h\) denote the height. Then, \(b=6 \ cm\) and \(h=10 \ cm\).
Substituting the values in the area of the right-angled triangle formula, we have:
Area, \(A=\frac{1}{2}(b \times h)\)
\(A=\frac{1}{2}(6 \times 10)\) \(sq. cm\)
\(A=\frac{1}{2}\times 60\) \(sq. cm\)
\(A=30 \ sq. cm\)
Therefore, the area of the right-angled triangle is \(30\) \(sq. \ cm\).
Register for free to see more content