UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreNow, we shall find the perimeter of a triangle.
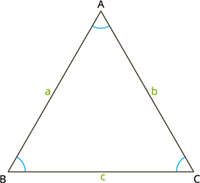
Let \(ABC\) be a triangle with sides of length \(a\), \(b\) and \(c \) \(units\).
Then, the perimeter of the triangle \(ABC\) is given by:
Perimeter of the triangle \(=\) Sum of the measures of all three sides
Perimeter \(P = AB+BC+CA\) \(units\)
\(P = a+c+b\) \(units\)
Therefore, the perimeter of the triangle is \(P = a+b+c\) \(units\).
Example:
1. The sides of the triangle are \(7 \ cm\), \(8 \ cm\) and \(10 \ cm\). Find the perimeter of the triangle.
Solution:
Let \(a\), \(b\) and \(c\) denote the sides of the triangle. Then, \(a = 7 \ cm\), \(b = 8 \ cm\) and \(c = 10 \ cm\).
Perimeter of the triangle \(=\) Sum of the measures of all three sides
Substituting the values in the formula, we have:
Perimeter, \(P = a+b+c\)
\(P = 7+8+10\) \(cm\)
\(P = 25 \ cm\)
Thus, the perimeter of the triangle is \(25 \ cm\).
Let us find the perimeter of an equilateral triangle.
A triangle in which all three sides were in the equal length is called the equilateral triangle.
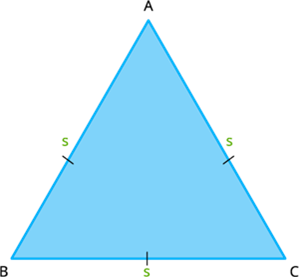
Let \(ABC\) be an equilateral triangle which has sides of length \(a\) units.
We know that the formula to find the perimeter of the triangle is \(P = a+b+c\), where \(a\), \(b\), \(c\) are the lengths of three sides of the triangle.
Since for an equilateral triangle, all the sides were equal, then substituting \(a = b = c = s\) in the formula of the perimeter of the triangle, we have:
Perimeter, \(P = s+s+s\) \(units\)
Therefore, the perimeter of the equilateral triangle is \(P = 3s\), where \(s\) is the length of three equal sides.
Example:
1. The side length of an equilateral triangle is \(9 \ cm\). Find the perimeter of an equilateral triangle.
Solution:
The side length of an equilateral triangle is \(s = 9\) \(cm\).
Perimeter \(= 3s\), where \(s\) is the length of three equal sides.
Substituting the value of \(s\) in the above formula, we have:
Perimeter \(= 3 \times 9\) \(cm\)
Perimeter \(= 27\) \(cm\)
Therefore, the perimeter of an equilateral triangle is \(27 \ cm\).
Register for free to see more content