Geometrical proof of identity - IV — lesson. Mathematics State Board, Class 7.

UPSKILL MATH PLUS

Learn Mathematics through our AI based learning portal with the support of our Academic Experts!

Identity \(- 4\):

(a + b)(a - b)= a^{2} - b^{2}

Let us first, simplify the identity

(a + b)(a - b)= a^{2} - b^{2}

Multiply the expression, as shown below.

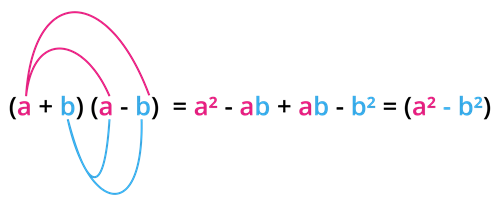
Now, we construct a figure to understand the concept.

Then we construct a rectangle using the above information.

In the given figure, \(AB = AD = a\).

So, the area of square \(ABCD = a^2\).

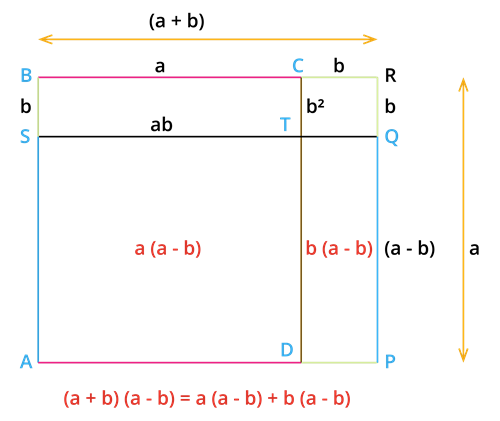
Also, \(SB = DP = b\). Then the area of the rectangle \(SBCT = ab\).

Similarly, the area of the rectangle \(DPRC = ab\). And the area of the square \(TQRC = b^2\).

Area of the rectangle \(DPQT = ab − b^2\).

Hence, \(\text{the area of the rectangle APQS = The area of square ABCD}\) \(\text{– area of rectangle STCB}\) \(\text{+ area of rectangle DPQT}\).

\begin{array}{l} = a^{2} - ab + (ab - b^{2}) \\ = a^{2} - ab + ab - b^{2} \\ = a^{2} - b^{2} \end{array}

Therefore,

(a + b)(a - b)= a^{2} - b^{2}

Example:

Simplify

(5 x + 7)(5 x - 7)

using the identity.

First, develop the given

(5 x + 7)(5 x - 7)

expression using the identity

(a + b)(a - b)= a^{2} - b^{2}

Here, \(a = 5x\); \(b = 7y\).

\begin{array}{l} (5 x + 7)(5 x - 7) = {(5 x)}^{2} - {(7)}^{2} \\ = 5^{2} \times x^{2} - {(7)}^{2} \\ = 25 x^{2} - 49 \end{array}

Therefore,

(5 x + 7)(5 x - 7)

\(=\) 25\(x^2 -\)49.

Did you find an error?

6. Geometrical proof of identity - IV