Sum of the angles around a point — lesson. Mathematics State Board, Class 7.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

Linear pair:

Linear pair of angles should add up to \(180°\).

If the given two adjacent angles does not make the \(180°\), then it is not a linear pair.

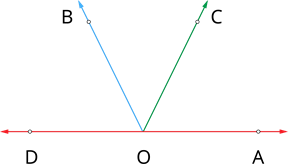
We studied that the sum of all the angles formed at a point on a straight line is \(180°\).

Think what would be the angle if many rays arises from a single point!

All the rays are starting from a single point. So the sum of the angles around a point will be \(360°\).

Now we understand this with some example.

Observe the below figure. Here \(AB\) is a straight line. And \(OC\) is a ray meeting \(AB\) at \(O\). It is evident that

∠ AOC

and

∠ BOC

is a linear pairs, so it makes the angles of \(180°\).

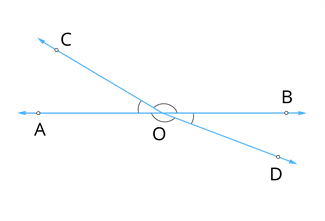
Also the another ray \(OD\) meeting \(AB\) at \(O\). Then

∠ AOD

and

∠ BOD

is a linear, which makes \(180°\).

We can observe that all the angles

∠ AOC

∠ BOC

∠ AOD

and

∠ BOD

are originated at the point of \(O\).

Therefore,

(∠ AOC + ∠ BOC) + (∠ AOD + ∠ BOD) = 180 ° + 180 ° = 360 °

Hence, it is clear that the sum of the angles at a point will be \(360°\).

Did you find an error?

3. Sum of the angles around a point