PDF chapter test TRY NOW
Illustration:
Consider a triangle \(ABC\) right angled at \(A\) with its hypotenuse \(BC\) at its base.
Draw an altitude to the triangle as follows:
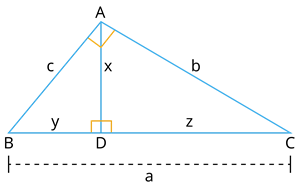
Two smaller right triangles \(ABD\) and \(ACD\) are obtained.
Now, all the three triangles \(ABC\), \(ADB\) and \(ADC\) are similar.
Based on this similarity, the following theorem is obtained.
Statement:
If an altitude is drawn to the hypotenuse of an right angled triangle, then:
(i) The two triangles are similar to the given triangle and also to each other.
That is, \(\Delta ABC \sim \Delta ADB \sim \Delta ADC\).
(ii) \(x^2 = yz\)
(iii) \(b^2 = za\) and \(c^2 = ya\) where \(a = y + z\)
Example:
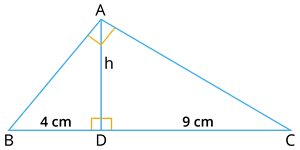
From the figure, find the altitude \(h\).
Solution:
By the statement (ii) of the Altitude-on-Hypotenuse theorem, the altitude is computed as follows:
\(h^2 = BD \times DC\)
\(h^2 = 4 \times 9\)
\(h^2 =\) \(36\)
\(\Rightarrow h = \sqrt{36}\)
\(= 6\)
Therefore, the measure of the altitude is \(6\) \(cm\).
Register for free to see more content