
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoStatement:
In a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
Explanation:
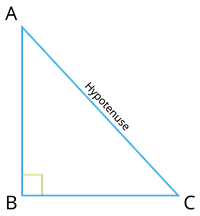
The theorem states that in the right angled triangle ABC, AC^2=AB^2+BC^2.
Proof of the theorem:
Given:
A triangle right angled at B.
That is \angle ABC = 90^{\circ}.
To prove:
AC^2=AB^2+BC^2
Construction:
Construct a line from B to AC to intersect at D such that BD \perp AC.
Proof:
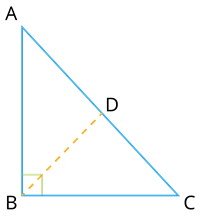
Consider the triangles ABC and BDC.
The \angle C is common to both the triangles.
Since BD \perp AC we have \angle BDC = 90^{\circ}.
Also, given that \angle ABC = 90^{\circ}.
Thus by AA similarity (If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar) it is concluded that the triangles ABD and BDC are similar.
Therefore, the ratio of the corresponding sides of the triangles are equal.
That is, \frac{BC}{CD} = \frac{AC}{BC}.
This implies, BC^{2} = AC \times CD ……(1)
Now consider the triangles ABC and ABD.
Similarly by AA criterion, the two triangles are similar.
So, \frac{AB}{AD} = \frac{AC}{AB}.
This implies, AB^{2} = AC \times AD ……(2)
Add equations (1) and (2) as follows:
BC^2 + AB^2 = (AC \times CD) + (AC \times AD)
= AC (CD +AD)
= AC \cdot AC
= AC^2.
Therefore, AC^2 = AB^2 + BC^2.
Hence, the proof.
Example:
In a right angled triangle, if the measure of the hypotenuse is 29 cm and one of its side is 21 cm then, find the length of the other side.
Solution:
Let the triangle be ABC right angled at B.
This implies that the side AC is the hypotenuse.
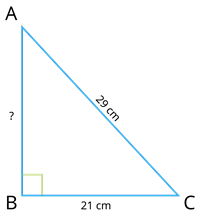
By the Pythagorean theorem, we have AC^2 = AB^2 + BC^2.
Thus, AB^2 = AC^2 - BC^2.
\Rightarrow AB^2 = 29^2 -21^2
= 841 - 441
= 400
Hence, AB = \sqrt{400}.
AB = 20
Therefore, the length of the other side is 20 cm.