Two mark exercise problems — task. Mathematics State Board, Class 8.

PDF chapter test TRY NOW

1. Is

$\triangle PRQ \equiv \triangle QSP$ ? Why?

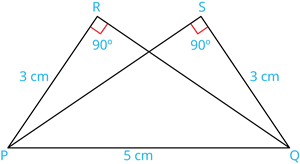
Proof:

	Statements	Reason
(i)	$\angle PRQ = \angle PSQ = 90^{\circ}$
(ii)	$PR = QS = 3 \ cm$
(iii	$PQ = PQ = 5 \ cm$
(iv)	$\triangle PRQ \equiv \triangle QSP$

2. In the figure, given that

$\angle 1 \equiv 2$ and

$\angle 3 \equiv \angle 4$ . Prove that

$\triangle MUG \equiv \triangle TUB$ .

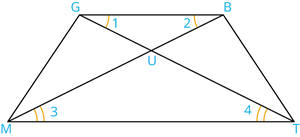
Proof:

	Statements	Reason
(i)	$MU = TU$	Since $\angle 3 = \angle 4$ then
(ii)	$UG = UB$	Since $\angle 1 = \angle 2$ then
(iii)	$\angle GUM = \angle BUT$
(iv)	$\triangle MUG \equiv \triangle TUB$	(1, 2, 3)

Answer variants:

vertically opposite angles

common

by SSS congruence

given

opposite sides of equal angles are equal

by RHS congruence

by SAS congruence

Did you find an error?

4. Two mark exercise problems