UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn more- Draw a side and make an angle that is given with side measure.
- Make a new angle from the newly formed side (X-axis).
- Make the given angle another. This would intersect with the axis of Y formed above. The quadrilateral is to be formed.
Example:
Construct a quadrilateral PLAN with following measurements.
PL = 4 cm, LA = 6.5 cm, ∠P= 90°, ∠A = 110°, ∠N = 85°
The sum of the angles of a quadrilateral is 360°. So, ∠P + ∠L + ∠A + ∠N = 360°.
90° + ∠L + 110° + 85° = 360°
90° + ∠L + 195° = 360°
∠L + 285° = 360°
∠L = 360° - 285°
∠L = 75°
Step 1: Draw the side PL = 4 cm and draw the angle 75 ° at the point L. As the vertex A is 6.5 cm away from L, cut the line segment LA of 6.5 cm out from this ray.
Step 2: Again, draw the angle 110 ° at the point A.
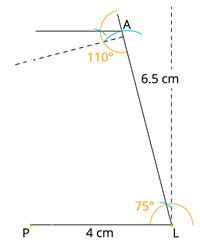
Step 3: Draw the angle 90 ° at the point P. This ray will meet the previously drawn A ray at the N point.
Thus, the required quadrilateral PLAN has been constructed.
Register for free to see more content