PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIf \(\angle E = \angle S\) and \(G\) is the midpoint of \(ES\), prove that \(\triangle GET \equiv \triangle GST\).
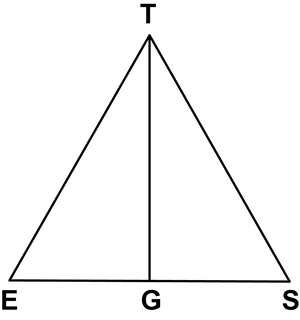
Proof:
| Statements | Reasons | |
| (i) | \(\angle E \equiv \angle S\) | |
| (ii) | \(ET \equiv ST\) | |
| (iii) | \(G\) is the midpoint of \(ES\) | |
| (iv) | \(EG \equiv SG\) | |
| (v) | \(TG \equiv TG\) | |
| (vi) | \(\triangle GET \equiv GST\) |
Answer variants:
vertical angles are congruent
given
by ASA(1,3,5)
if angles, then sides
follows from 1 and 4
by SSS(2, 4, 5) and also by SAS(2, 1, 4)
By reflexive property
follows from 3
Register for free to see more content