PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIn the given figure, \(UB \parallel AT\) and \(CU \equiv CB\). Prove that \(\triangle CUB \sim \triangle CAT\) and hence \(\triangle CAT\) is isosceles.
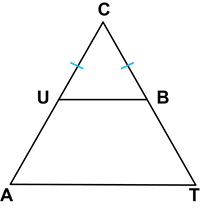
Proof:
| Statements | Reasons | |
| 1 | \(\angle CUB = \angle CBU\) | |
| 2 | \(\angle CUB = \angle CAT\) | |
| 3 | \(\angle CBU = \angle CTA\) | |
| 4 | \(\angle UCB = \angle ACT\) | |
| 5 | \(\triangle CUB \sim \triangle CAT\) | |
| 6 | \(CA = CT\) | |
| 7 | \(\triangle CAT\) is an isosceles triangle |
Answer variants:
By AAA Similarity criteria(1,2,4)
Common angle
Since \(\angle CUB = \angle CBU\) and \(\angle CAT = \angle CTA\)
Given that \(UB \parallel AT\), corresponding angles are equal if \(CA\) is transversal.
By AAA Similarity criteria(1,2,3)
Given that in \(\triangle CUB\), \(CU = CB\).
Given that \(UB \parallel AT\), corresponding angles are equal if \(CT\) is transversal.
By AAA Similarity criteria(2,3,4)
Opposite sides of equal angle are equal.
Register for free to see more content