Four mark exercise problems IV — task. Mathematics State Board, Class 8.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

In the given figure,

$D$ is the midpoint of

$OE$ and

$\angle CDE = 90^{\circ}$ . Prove that

$\triangle ODC \equiv \triangle EDC$ .

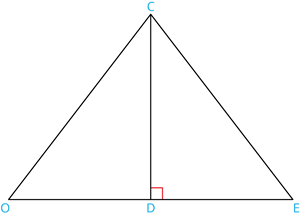
Proof:

	Statement	Reason
1	$OD = ED$
2	$DC = DC$
3	$\angle CDE = \angle CDO = 90^{\circ}$
4	$\triangle ODC \equiv \triangle EDC$

Answer variants:

Given that

$D$ is the midpoint of

$OE$ .

Common leg

Given that

$\angle CDE = 90^{\circ}$ and

$ODE$ is linear pair.

By SAS Criteria (1,2,3)

By RHS Criteria (1,2,3)

Did you find an error?

20. Four mark exercise problems IV