UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreThe perimeter of a rectangle: The perimeter is the total distance around the outside, that can be created by adding together the length and the breadth of each side.
Let us consider a rectangle \(ABCD\) of length '\(l\)' units and breadth '\(b\)' units.
The perimeter of the rectangle is therefore as follows:
Perimeter(\(P\)) \(=\) \((AB + BC + CD + DA)\) units.
\(P =\) \(( l + b + l + b )\) units.
\(P =\) \((2l + 2b)\) units.
\(P =\) \(2 (l + b)\) units.
Thus, the length of the rectangle given its perimeter is \(l = P/2 - b\) units.
And, the breadth of the rectangle given its perimeter is \(b = P/2 - l\) units.
Area of rectangle: The area of a rectangle is given by multiplying the length and the breadth.
Let us consider a rectangle \(ABCD\) of length '\(l\)' units and breadth '(b\)' units.
Therefore, the area of the rectangle is as follows:
Area (\(A\)) \(=\) length \(l\) \(×\) breadth \(b\).
Thus, the length of the rectangle given its area is \(l = A/b\) units.
And, the breadth of the rectangle given its area is \(b = A/l\) units.
Diagonals f rectangle: A rectangle has two diagonals they are equal in length and intersect in the middle. The diagonal is the square root of (length squared + breadth squared).
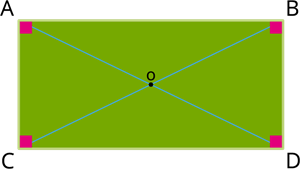
Diagonal \((d) =\) .
Where '\(l\)' and '\(b\)' is the length and breadth of the rectangle.
Register for free to see more content