Solving by cross multiplication method — lesson. Mathematics State Board, Class 9.

PDF chapter test TRY NOW

Let us consider two linear equations.

$a_1x+b_1y+c_1 = 0$ ----- (

$1$ )

$a_2x+b_2y+c_2 = 0$ ----- (

$2$ )

Where

$\frac{a_1}{a_2}\neq \frac{b_1}{b_2}$ .

Now, let us solve these two equations.

Multiply equation (

$1$ ) by

$b_2$ and equation (

$2$ ) by

$b_1$ .

Thus, we have:

$\begin{array}{l} a_{1} b_{2} x + b_{1} b_{2} y + b_{2} c_{1} = 0 \\ \underline{(-) a_{2} b_{1} x + b_{1} b_{2} y + b_{1} c_{2} = 0} \\ x (a_{1} b_{2} - a_{2} b_{1}) + b_{2} c_{1} - b_{1} c_{2} = 0 \end{array}$

$x(a_1b_2-a_2b_1) =$

$b_1c_2-b_2c_1$

$x=\frac{(b_1c_2-b_2c_1)}{(a_1b_2-a_2b_1)}$

Similarly, let us multiply equation (

$1$ ) by

$a_2$ and equation (

$2$ ) by

$a_1$ .

Thus, we have:

$\begin{array}{l} a_{1} a_{2} x + b_{1} a_{2} y + c_{1} a_{2} = 0 \\ \underline{(-) a_{1} a_{2} x + b_{2} a_{1} y + c_{2} a_{1} = 0} \\ 0 + y (b_{1} a_{2} - b_{2} a_{1}) + c_{1} a_{2} - c_{2} a_{1} = 0 \end{array}$

$y(b_1a_2-b_2a_1) =$

$c_2a_1-c_1a_2$

$y=\frac{(c_2a_1-c_1a_2)}{(b_1a_2-b_2a_1)}$

Therefore, the solution to the given system of linear equations is

$x = \frac{(b_1c_2-b_2c_1)}{(a_1b_2-a_2b_1)}$ and

$y = \frac{(c_1a_2-c_2a_1)}{(b_1a_2-b_2a_1)}$ .

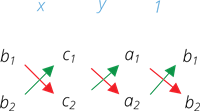
The other way to represent the solution is given by:

$\frac{x}{b_1c_2-b_2c_1} = \frac{y}{c_1a_2-c_2a_1}$

$= \frac{1}{a_1b_2-a_2b_1}$

It can easily remembered as:

Let us consider an example to understand the concept clearly.

Example:

Solve the simultaneous linear equations

$2x+y = 8$ and

$x+2y = 10$ by cross multiplication method.

Solution:

Let us write the given equations in the form of

$ax+by+c = 0$ .

$2x+y-8 = 0$ ---- (

$1$ )

$x+2y-10 = 0$ ---- (

$2$ )

Now, let us write the coefficients in the form of

Thus, we have:

$\frac{x}{(1)(-10)-(2)(-8)}=$

$\frac{y}{(-8)(1)-(-10)(2)} =$

$\frac{1}{(2)(2)-(1)(1)}$

$\frac{x}{-10-(-16)} = \frac{y}{-8-(-20)} =$

$\frac{1}{4-1}$

$\frac{x}{-10+16} = \frac{y}{-8+20}=\frac{1}{3}$

$\frac{x}{6} = \frac{y}{12}=\frac{1}{3}$

$\frac{x}{6} = \frac{1}{3}$ and

$\frac{y}{12} = \frac{1}{3}$

$x = \frac{6}{3}$ and

$y = \frac{12}{3}$

$x = 2$ and

$y = 4$

Therefore, the solution is

$x = 2$ and

$y = 4$ .

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

8. Solving by cross multiplication method

Theory: