PDF chapter test TRY NOW
x-co-ordinate of a point:
The x-coordinate of a point is the perpendicular distance from the y-axis measured along the x-axis.
y-co-ordinate of a point:
The y-coordinate of a point is the perpendicular distance from the x-axis measured along the y-axis.
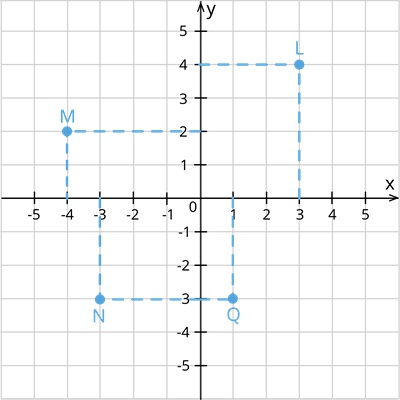
1. The perpendicular distance of the point L from the y-axis measured along the positive direction of the y-axis is LX=4 units and the perpendicular distance of the point L from the x-axis measured along the positive direction of the x-axis OL=3 units.
Point L lies at the first quadrant in the above graph; hence its co-ordinates will be represented as (x, y), where x=3 and y=4 is the co-ordinate of L in cartesian plane is represented as (3,4).
2. The perpendicular distance of the point M from the y-axis measured along the positive direction of the y-axis is MX'=2 units and the perpendicular distance of the point M from the x-axis measured along the negative direction of the x-axis OM=2 units.
Point M lies at the second quadrant in the above graph; hence its co-ordinates will be represented as (-x, y), where x=4 and y=2 is the co-ordinate of M in cartesian plane is represented (-4,2).
3. The perpendicular distance of the point N from the y-axis measured along the negative direction of the y-axis is NX'=3 units and the perpendicular distance of the point N from the x-axis measured along the negative direction of the x-axis OX'=2 units.
Point N lies at the third quadrant in the above graph; hence its co-ordinates will be represented as (-x, -y), where x=2 and y=3 is the co-ordinate of L in cartesian plane is represented as (-2,-3).
4. The perpendicular distance of the point Q from the y-axis measured along the negative direction of the y-axis is QX=3 units and the perpendicular distance of the point Q from the x-axis measured along the positive direction of the x-axis OX = 1 unit.
Point Q lies at the fourth quadrant in the above graph; hence its co-ordinates will be represented as (x, -y), where x=1 and y=3 is the co-ordinate of L in cartesian plane is represented as (1,-3).
Important!
Measure the positive coordinate value along the positive direction of the axis and the negative coordinate value along the negative direction of the axis.
