How to represent square roots of real numbers geometrically — lesson. Mathematics State Board, Class 9.

PDF chapter test TRY NOW

Let us recall the concept of the square number we learned so far.

If '\(a\)' is a natural number, then

\sqrt{a}

\(= b\). That is, \(b² = a\) and \(b > 0\).

We are now going to extend the same definition to positive real numbers.

If \(a > 0\) be a real number, then

\sqrt{a}

\(= b\). That is, \(b² = a\) and \(b > 0\).

Let us learn how to find

\sqrt{x}

for any given positive real number '\(x\)' geometrically.

The general procedure to represent

\sqrt{x}

geometrically:

Step 1: If the given positive number is '\(x\)' we have to mark '\(B\)' so that \(AB = x\) units.

Step 2: From point '\(B\)', mark a distance of \(1\) unit and label the point as '\(C\)'. That is \(BC =1\) unit.

Step 3: Now find the midpoint of \(AC\) and mark the midpoint as '\(O\)'.

Step 4: Draw a semicircle with centre '\(O\)' and radius \(OC\).

Step 5: Draw a line perpendicular to \(AC\) which passes through point '\(B\)' and intersect the semicircle at '\(D\)' such that \(∠OBD = 90°\).

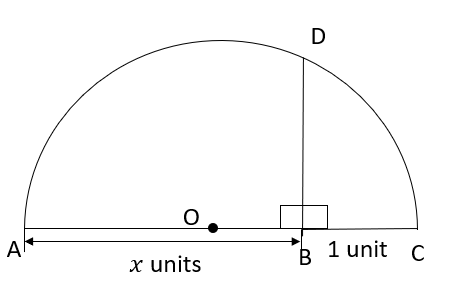
Step 6: Now measure the length of \(BD\), which is nothing but

\sqrt{x}

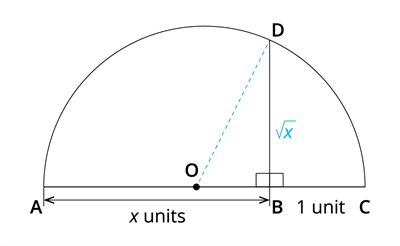
Let us verify the value by applying Pythagoras theorem.

Consider the right triangle \(OBD\).

\(OD²=OB²+BD²\)

We know that \(OD = OC\)(radius).

Here \(AC = AB +BC = x+1\). So \(OC = (x+1)/2 = OD\) .

Then \(OB = OC - 1 = (x+1)/2 -1 = (x-1)/2\).

\begin{array}{l} BD = \sqrt{{OD}^{2} - {OB}^{2}} \\ BD = \sqrt{{(\frac{x + 1}{2})}^{2} - {(\frac{x - 1}{2})}^{2}} \\ BD = \sqrt{\frac{x^{2} + 1 + 2 x - x^{2} - 1 + 2 x}{4}} \\ BD = \sqrt{\frac{4 x}{4}} \\ BD = \sqrt{x} \end{array}

Thus, the length of \(BD\) gives the value of

\sqrt{x}

Example:

Now we will try to find square root for the number \(4.6\)

Step 1: If the given positive number is '\(x\)' we have to mark '\(B\)' so that \(AB = 4.6\) units.

Step 2: From point '\(B\)', mark a distance of \(1\) unit and label the point as '\(C\)'. That is \(BC =1\) unit.

Step 3: Now find the midpoint of \(AC = 4.6+1 = 5.6\) units and mark the midpoint as '\(O\)'.

Step 4: Draw a semicircle with centre '\(O\)' and radius \(OC =5.6/2 = 2.8\) units.

Step 5: Draw a line perpendicular to \(AC\) which passes through point '\(B\)' and intersect the semicircle at '\(D\)' such that \(∠OBD = 90°\).

Step 6: Now measure the length of \(BD = 2.145\) which is nothing but

\sqrt{x}

Let us verify the value by applying Pythagoras theorem.

Consider the right triangle \(OBD\).

\(OD²=OB²+BD²\)

We know that \(OD = OC = 2.8\) (radius).

Now \(OB = OC - BC = 2.8-1 = 1.8\) units.

\begin{array}{l} BD = \sqrt{{OD}^{2} - {OB}^{2}} \\ BD = \sqrt{{(2.8)}^{2} - {(1.8)}^{2}} \\ BD = \sqrt{7.84 - 3.24} \\ BD = \sqrt{4.6} \\ BD = 2.145 \end{array}

Did you find an error?

5. How to represent square roots of real numbers geometrically