30. Five mark exercise problems VI

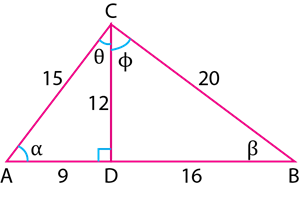
1. From the given figure, prove that \(\theta + \phi = 90^{\circ}\). Also prove that there are two other right angled triangles. Find \(sin \ \alpha\), \(cos \ \beta\) and \(tan \ \phi\).

 

 

Answer:

 

\(sin \ \alpha =\) $\frac{i}{i}$

 

\(cos \ \beta =\) $\frac{i}{i}$

 

\(tan \ \phi =\) $\frac{i}{i}$

 

2. Verify \(cos \ 90^{\circ} = 1 - 2 \ sin^2 \ 45^{\circ} = 2 \ cos^2 \ 45^{\circ} - 1\)

 

Proof:

 

\(cos \ 90^{\circ} =\)

 

\(1 - 2 \ sin^2 \ 45^{\circ} =\)

 

\(2 \ cos^2 \ 45^{\circ} - 1 =\)

 

Thus, \(cos \ 90^{\circ} = 1 - 2 \ sin^2 \ 45^{\circ} = 2 \ cos^2 \ 45^{\circ} - 1\).

 

Hence, we proved.