
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demo1. Make a parallel combination, \(XY\), of three resistors having resistances \(R_1\), \(R_2\) and \(R_3\), respectively. Connect it with a battery, a plug key and an ammeter, as shown in figure.
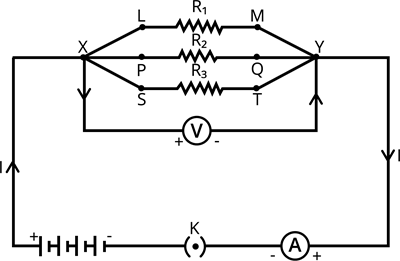
Circuit diagram
2. Also connect a voltmeter in parallel with the combination of resistors. Plug the key and note the ammeter reading.
3. Let the current be \(I\). Also take the voltmeter reading. It gives the potential difference \(V\), across the combination. The potential difference across each resistor is also \(V\). This can be checked by connecting the voltmeter across each individual resistor (see in the below figure).
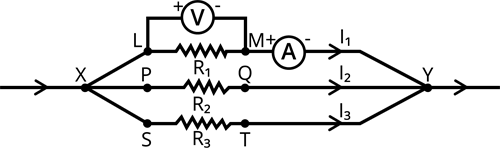
Circuit diagram
4. Take out the plug from the key. Remove the ammeter and voltmeter from the circuit. Insert the ammeter in series with the resistor \(R_1\), as shown in the above figure. Note the ammeter reading, \(I_1\).
5. Similarly, measure the currents through \(R_2\) and \(R_3\). Let these be \(I_2\) and \(I_3\), respectively.
What is the relationship between \(I\), \(I_1\), \(I_2\) and \(I_3\)?
According to Ohm's law, the current \(I_1\), \(I_2\) and \(I_3\) are given as
Total current passing through the circuit is
Substituting the values of \(I_1\), \(I_2\) and \(I_3\) in the above equation, we get the effective resistance \(R_P\) as
On combining the above equations, we get