PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoவிளக்கம் 1:
\(A\) மற்றும் \(B\) கணங்களை எடுத்துக்கொள்ளலாம்.
\(A\) \(=\) \(\{2, 3\}\) மற்றும் \(B\) \(=\) \(\{1, 2, 3\}\).
அதன் பெருக்கல் \(A \times B\) யை காண்போம்:
\(A \times B\) \(=\) \(\{(2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)\}\)
\(A \times B\) இன் வரைகலை விளக்கம்:
 |
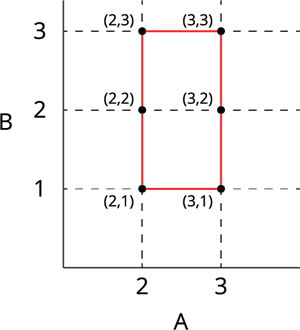அதேபோல், \(B \times A\) இன் பெருக்கலை காணலாம்:
\(B \times A\) \(=\) \(\{(1, 2), (1, 3), (2, 2), (2, 3), (3, 2), (3, 3)\}\)
\(B \times A\) இன் வரைகலை விளக்கம்:
 |
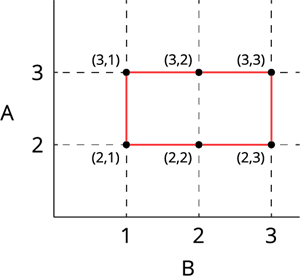\(A \times B\) மற்றும் \(B \times A\) வரைபடங்களிலிருந்து, \(A \times B\) \(\neq\) \(B \times A\) என்பதை கவனிக்கலாம்.
- பொதுவாக, \(A \times B\) \(\neq\) \(B \times A\) ஆனால் \(n(A \times B)\) \(=\) \(n(B \times A)\).
- \(A \times B = \phi\) எனில் \(A = \phi\) அல்லது \(B = \phi\).
- \(n(A) = x\) மற்றும் \(n(B) = y\) எனில்,\(n(A \times B) = xy\).
Important!
விளக்கம் 2:
\(A\) மற்றும் \(B\) கணங்களை எடுத்துக்கொள்ளலாம்.
\(A\) \(=\) \(\{\)\(\text{இடைவெளி}\) \( [2, 5]\)\( \text{இன் உள் உள்ள அனைத்து எண்களின் கணம்}\}\) and \(B\) \(=\) \(\{\text{இடைவெளி }\) \([4, 5]\) \(\text{இன் உள் உள்ள அனைத்து எண்களின் கணம்}\}\).
பெருக்கல் \(A \times B\) என்பது கொடுக்கப்பட்ட இடைவெளிகளின் வெட்டும் பகுதிக்கு ஒத்திருக்கிறது. வேறு வார்த்தைகளில் கூறுவதானால், இது பொதுவான பகுதிக்குள் இருக்கும் அனைத்து புள்ளிகளின் \((x,y)\) தொகுப்பு. என்பது கொடுக்கப்பட்ட இடைவெளிகளின் வெட்டும் பகுதிக்கு ஒத்திருக்கிறது.
பெருக்கல் \(A×B\) ஐ பின்வருமாறு விளக்குவோம்:
 |
பெருக்கல் \(A×B\) நடுத்தர செவ்வக பகுதிக்கு ஒத்திருக்கிறது. அதாவது, இந்த செவ்வகப் பகுதியில் உள்ள அனைத்து புள்ளிகளையும் \((x,y)\) கொண்டுள்ளது.
Important!
பெருக்கல் \(\mathbb{R} \times \mathbb{R}) கார்ட்டீசியன் தளம் என்று அழைக்கப்படுகிறது, இது அனைத்து புள்ளிகளின் \((x,y)\) தொகுப்பைக் குறிக்கிறது, அங்கு \(x\), \(y\) மெய்யென் ஆகும்.
Register for free to see more content