PDF chapter test TRY NOW
இந்த பக்கத்தில் இரண்டு கணங்களின் கார்ட்டீசியன் பெருக்கலை பற்றி அறிந்து கொள்வோம்.
விளக்கம்:
\(A\) மற்றும் \(B\) கணங்களை கருத்தில் கொள்வோம்.இங்கே \(A\) என்பது \(1\), \(2\) மற்றும் \(3\) என்ற சிறுவர்களின் கணம் ஆகும்.
அதாவது, \(A\) \(=\) \(\{1,2,3\}\).
மற்றும் \(B\) என்பது \(a\), \(b\) மற்றும் \(c\) என பெயரிடப்பட்ட சிறுமிகளின் கணம் ஆகும்.
அதாவது, \(B\) \(=\) \(\{a,b,c\}\).
அம்புக்குறி வரைபடத்தைப் பயன்படுத்தி நடன நிகழ்ச்சிக்காக ஒவ்வொரு சிறுவனயும் ஒரு சிறுமியுடன் இணைப்பதற்கான சாத்தியமான வழிகளைப் பார்ப்போம்.
 |
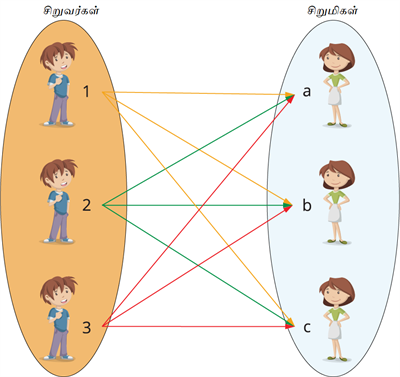கீழே கொடுக்கப்பட்டுள்ளபடி நாம் \(9\) வெவ்வேறு சோடிகளைத் தேர்ந்தெடுக்கலாம்:
| \((1,a), (1,b), (1,c), (2,a), (2,b), (2,c), (3,a), (3,b), (3,c)\) |
இங்கே, இந்த சோடிகள் சிறுவர்கள் மற்றும் சிறுமிகளின் கணங்களின் கார்ட்டீசியன் பெருக்கலை குறிக்கின்றன.
மேலே உள்ள விளக்கத்தின் அடிப்படையில், \(A\) மற்றும் \(B\) கண்களின் கார்ட்டீசியன் பெருக்கலை பின்வருமாறு வரையறுப்போம்::
வரையறை:
\(A\) மற்றும் \(B\) என்பன இரண்டு வெற்றில்லா கணங்கள் எனில், இவற்றின் வரிசைச் சோடிகளின் கணமானது \((a, b)\) அதாவது \(a\in A\) , \(b\in B\) என இருக்கும். இதை \(A\) மற்றும் \(B\)-யின்
கார்டீசியன் பெருக்கல் என்கிறோம். எனவே, \(A\times B\) ́\(=\) \(\{(a, b )| a ∈ A, b ∈B \}\) . \(A\times B\) என்பதை (\(A\) கிராஸ் \(B\)) எனப் படிக்கவும்.
கார்டீசியன் பெருக்கல் என்கிறோம். எனவே, \(A\times B\) ́\(=\) \(\{(a, b )| a ∈ A, b ∈B \}\) . \(A\times B\) என்பதை (\(A\) கிராஸ் \(B\)) எனப் படிக்கவும்.
Important!
- \(A × B\) என்பது, \(A\) மற்றும் \(B\) என்ற கணங்களுக்கிடையேயான அனைத்து வரிசைச் சோடிகளின் கணம் எனில், அதன் முதல் உறுப்பு \(A\)-யின் உறுப்பாகவும், இரண்டாவது உறுப்பு \(B\)-யின் உறுப்பாகவும் இருக்கும்.
- \(B × A\) என்பது, \(A\) மற்றும் \(B\) என்ற கணங்களுக்கிடையேயான அனைத்து வரிசைச் சோடிகளின் கணம் எனில், முதல் உறுப்பு \(B\)-யின் உறுப்பாகவும் இரண்டாவது உறுப்பு \(A\)-யின் உறுப்பாகவும் இருக்கும்.
- \(a = b\) எனில், \((a,b)=(b,a)\).
- \(A\), \(B\) மற்றும் \(C\) ஆகிய மூன்று கணங்களுக்கும், பின்வரும் பண்புகள் உண்மையாக இருக்கும்.
- \(A \times (B \cup C)\) \(=\) \((A \times B) \cup (A \times C)\) (சேர்ப்பு மீதான பங்கீட்டு பண்பு).
- \(A \times (B \cap C)\) \(=\) \((A \times B) \cap (A \times C)\) (வெட்டு மீதான பங்கீட்டு பண்பு).
Register for free to see more content