PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demo\(A\) மற்றும் \(B\) என்பன இரு கணங்கள் மேலும், \(R\) ஆனது \(A\) லிருந்து \(B\) க்கு செல்லும் உறவு ஆகும்.
இங்கு,
உறவு \(R\) இன் மதிப்பகம் ஏதேனும் ஒரு \(y \in B \}\)
உறவு \(R\) இன் துணை மதிப்பகம் \(=B\)
உறவு \(R\) இன் வீச்சகம் , ஏதேனும் ஒரு \(y ∈ A\}\)
மேற்கண்ட வரையரையிலிருந்து மதிப்பகம் \(\subseteq A\) மற்றும் வீச்சகம் ஆகும்.
இப்போது, அம்புக்குறி படத்தைப் பற்றி பார்க்கலாம்.
உறவைக் காட்சிப்படுத்தி அறிய அம்புக்குறி படத்தைப் பயன்படுத்தலாம்.
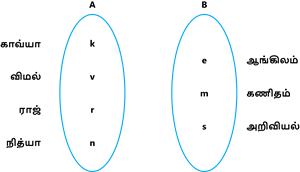
| மாணவர்கள் \(A\) | பாடங்கள் \(B\) |
| காவ்யா \(k\) | ஆங்கிலம் \(e\) |
| விமல் \(v\) | கணிதம் \(m\) |
| ராஜ் \(r\) | அறிவியல் \(s\) |
| நித்யா \(n\) |
என்பது ஒரு உறவு எனில் இதனை கீழ்கண்டவாறு அம்புக்குறி படம் மூலம் பார்க்கலாம்.
மேலும், \(A\) மற்றும் \(B\) இன் கார்டீசியன் பெருக்கல்:
மாணவர்களை தேர்வோடு இணைக்க கீழ்கண்டவாறு அம்புக்குறி படம் கிடைக்கும்.
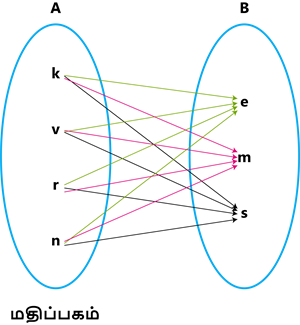
மதிப்பகம்:
கீழ்கண்ட படத்தில் \(A\) என்பது உறவின் மதிப்பகம் ஆகும்.
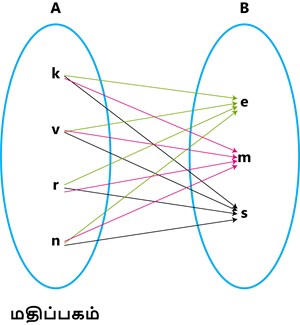
துணை மதிப்பகம்:
\(R\) என்ற உறவின் துணைமதிப்பகம் \(=B\).
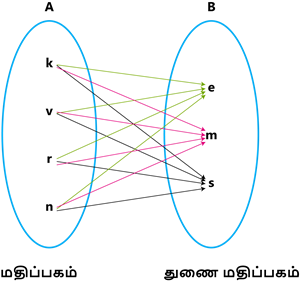
வீச்சகம்:
\(R\) இன் வீச்சகம் \(=\{e, m, s\}=R\) இன் துணை மதிப்பகம்.
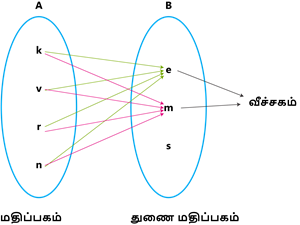
இங்கு, அறிவியல் படத்தை நீக்கினால் மதிப்பகம் மற்றும் துணை மதிப்பகம் சமம் ஆனால் வீச்சகம் மாறுவதைக் கீழ்கண்ட வரைபடத்தின் மூலம் அறியலாம்.
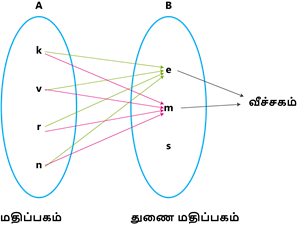
Example:
கீழ்கண்ட வரைபடம் \(A\) மற்றும் \(B\)யின் உறவை விளக்குகிறது எனில் கீழ்கண்ட வினாவிற்கு விடையளிக்க:
i) \(R\) இன் மதிப்பகம், வீச்சகம் மற்றும் துணை மதிபகம் என்ன?
ii) கார்டீசியன் பெருக்கல்
iii) பட்டியல் முறையில் எழுதுக
தீர்வு:
i) \(R\) இன் மதிப்பகம் \(=\) \(\{a, b, c, d\}\).
\(R =\) இன் துணை மதிப்பகம் \(\{1, 2, 3\}\).
\(R =\) இன் வீச்சகம் \(\{1, 2\}\).
ii) கார்டீசியன் பெருக்கல்:
\(A × B =\) \(\{(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3), (c, 1), (c, 2), (c, 3), (d, 1), (d, 2), (d, 3)\}\).
iii) பட்டியல் முறை:
\(R =\) \(\{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2), (d, 1), (d, 2)\}\).
Register for free to see more content