PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoசார்பு என்பது இரு வெற்றற்ற கணங்களுக்கிடையே உள்ள உறவாகும்.
கீழ்க்கண்ட எடுத்துக்காட்டைப் பார்க்கலாம்.
5 வீடுகள் மற்றும் அவற்றின் வாடகைகள் கீழே அம்புக்குறி படமாக கொடுக்கப்பட்டுள்ளன.
இதிலிருந்து, அனைத்து வீடுகளும் ஒரே ஒரு வாடகை மதிப்பைப் பெற்றிருப்பதை அறிய முடிகிறது.
Example:
சார்புகளைப் பற்றி அறிய கீழ்க்கண்ட எடுத்துக்காட்டுகளைக் காணலாம்.
1. ஒரு நாளின் சராசரி வெப்பம், ஒரே அளவாகத்தான் இருக்கும்.
2. ஒரு வகுப்பில் உள்ள மாணவர்கள் ஒவ்வொருவருக்கும் ஒரே ஒரு பதிவு எண் தான் இருக்க முடியும்.
சார்பு:
X மற்றும் Y என்ற வெற்றில்லா கணங்களுக்கிடையேயான ஒரு உறவு f-ல் ஒவ்வொரு x\in X -க்கும் ஒரே ஒரு y \in Y கிடைக்கிறது எனில், f ஐ நாம் “சார்பு” என்கிறோம்.
அதாவது, f =\{(x,y)| ஒவ்வொரு x \in X-க்கும், ஒரே ஒரு y \in Y இருக்கும்\}.
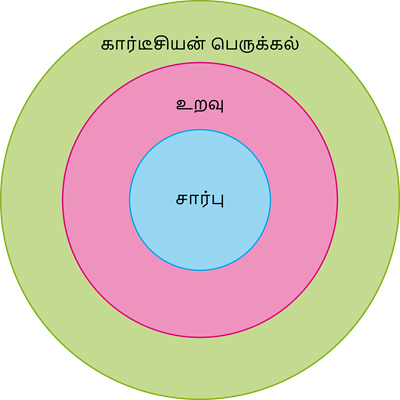
சார்புக்கும் உறவுக்கும் இடையே உள்ள தொடர்பு:
அனைத்து சார்புகளும் உறவாகும். ஆனால் அனைத்து உறவுகளும் சார்பு அல்ல.
1. சார்பு என்பது உறவின் உட்கணம் ஆகும்.
2. உறவு என்பது கார்டீசியன் பெருக்கலின் உட்கணம் ஆகும்.
கீழ்க்கண்ட படத்தின் மூலம் இதனைத் தெளிவாக அறியலாம்.
Example:
A = \{1,2,3\} மற்றும் B = \{1,4,9\} என்பன இரு கணங்கள் என்க. h என்ற உறவானது 'h(x) = x^2' என்றவாறு A லிருந்து B க்கு வரையறுக்கப்படுகிறது.
இந்த உறவானது சார்பா என, வரையறையைப் பயன்படுத்தி சரிபார்க்கலாம்.
இங்கு, A மற்றும் B என்பது வெற்றற்ற கணங்கள்.
மேலும்,
h(1) = (1)^2 = 1
h(2) = (2)^2 = 4
h(3) = (3)^2 = 9
இங்கு, A உள்ள ஒவ்வொரு உறுப்புக்கும் B இல் ஒரு உறுப்பு கிடைக்கிறது.
எனவே, (1,1), (2,4), (3,9) என்பது உறவாகும்.
Important!
- X லிருந்து Y க்கு உள்ள f என்ற சார்பை f : X \rightarrow Y என எழுதலாம்.
- ஒரு சார்பை, தொடர்புபடுத்துதல் அல்லது உருமாற்றம் செய்தல் எனக் கருதலாம்.
Register for free to see more content