PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demo\(f : X \rightarrow Y\) என்பது ஒரு சார்பு என்க.
1. மதிப்பகம் மற்றும் துணை மதிப்பகம்:
\(f : X \rightarrow Y\) என்ற சார்பில், \(X\) என்பது மதிப்பகம் மற்றும் \(Y\) என்பது துணை மதிப்பகம்.
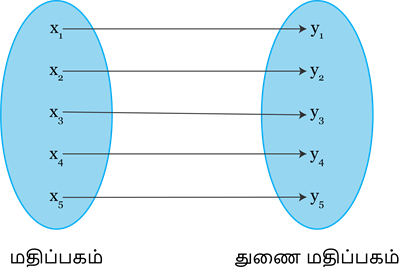
மதிப்பகம் \(=\) \(X\) \(=\) \(\{x_1\), \(x_2\), \(x_3\), \(x_4\), \(x_5\),\(...\}\)
துணை மதிப்பகம் \(=\) \(Y\) \(=\) \(\{y_1\), \(y_2\), \(y_3\), \(y_4\), \(y_5\),\(...\}\)
2. நிழல் உரு முன் உரு:
\(f(x) = y\) எனில் \(x\) இன் நிழல் '\(y\)' மற்றும் \(y\) இன் முன் உரு '\(x\)' ஆகும்.
மேற்கண்ட படத்திலிருந்து,
நிழல் \(y_1\) க்கு \(x_1\) முன் உரு.
நிழல் \(y_2\) க்கு \(x_2\) முன் உரு.
நிழல் \(y_3\) க்கு \(x_3\) முன் உரு.
நிழல் \(y_4\) க்கு \(x_4\) முன் உரு.
நிழல் \(y_5\) க்கு \(x_5\) முன் உரு.
3. சார்புகளுக்கான சோதனை:
\(f : X \rightarrow Y\) என்ற உறவு சார்பாக இருக்க வேண்டுமெனில், கீழ்க்கண்டவற்றை நிறைவு செய்ய வேண்டும்.
- மதிப்பகத்தில் உள்ள ஒவ்வொரு உறுப்பிற்கும் நிழல் உரு இருக்க வேண்டும்.
- ஒவ்வொரு உறுப்பிற்கும் ஒரே ஒரு நிழல் உருதான் இருக்க வேண்டும்.
Example:
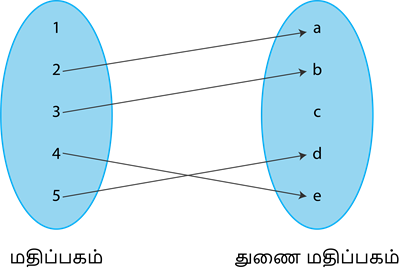
மேற்கண்ட வரைபடத்தில் மதிப்பகத்தில் உள்ள ஒவ்வொரு உறுப்புக்கும் துணை மதிப்பகத்தில் ஒரே ஒரு நிழல் உரு இருப்பதை காண முடிகிறது. எனவே, இது சார்பாகும்.
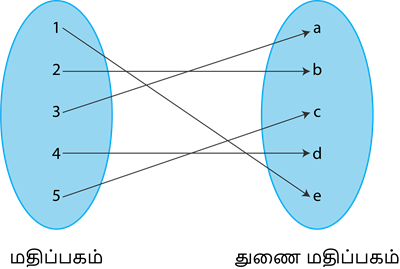
இங்கு, மதிப்பகத்தில் உள்ள \(1\) என்ற உறுப்புக்கு துணை மதிப்பகத்தில் நிழல் உரு இல்லை. எனவே, இது சார்பகம் அல்ல.
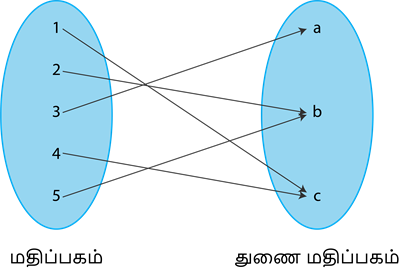
இங்கு, மதிப்பகத்தில் உள்ள அனைத்து உறவுக்கும் துணை மதிப்பகத்தில் ஒரே ஒரு நிழல் உரு உள்ளது. எனவே, இது சார்பகம் ஆகும்.
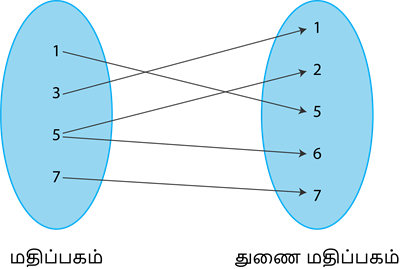
இங்கு மதிப்பகத்தில் உள்ள \(5\) என்ற உறுப்புக்கு \(2\) மற்றும் \(6\) என்ற இரண்டு நிழல் உருக்கள் உள்ளன. எனவே, இது சார்பு அல்ல.
வீச்சகம்::
அனைத்து நிழல்களின் கணம் வீச்சகம் ஆகும்.
மேற்கண்ட வரைபடத்திலிருந்து,
வீச்சகம் \(=\) \(\{y_1\), \(y_2\), \(y_3\), \(y_4\), \(y_5\}\)
Important!
\(n(K) = t\), மற்றும் \(n(L) = s\)
\(K\) லிருந்து \(L\) க்கு உள்ள சார்பகங்களின் எண்ணிக்கை \(s^t\) ஆகும்.
\(f : X \rightarrow Y\), \(n(X)\) \(=\) \(2\) மற்றும் \(n(Y)\) \(=\) \(3\) எனில்,
\(f\) இன் எண்ணிக்கை \(=\) \(n(Y)^{n(X)}\) \(=\) \(3^2\)
Register for free to see more content