PDF chapter test TRY NOW
சில சிறப்புவகை சார்புகளைப் பற்றி காணலாம்.
1. மாறிலிச் சார்பு
2. சமனிச் சார்பு
3. மெய் மதிப்புச் சார்பு
1. மாறிலிச் சார்பு
\(A \rightarrow B\) ஆனது மாறிலிச் சார்பு எனில், \(f\) -ன் வீச்சகமானது ஒரே ஓர் உறுப்பைக் கொண்டதாகும். அதாவது, \(A\) இன் எல்லா மதிப்புக்கும் \(B\) இல் ஒரே ஒரு நிழல் உரு மட்டுமே கிடைக்கும்.
Example:
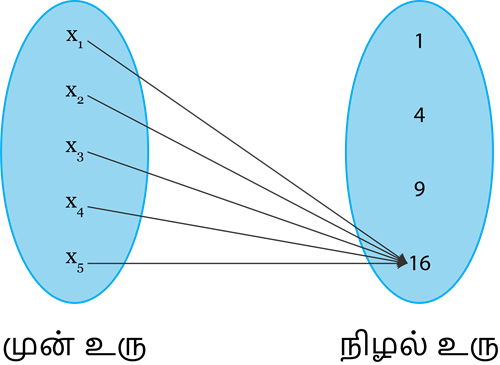
\(x_1\), \(x_2\), \(x_3\), \(x_4\) மற்றும் \(x_5\) ஆகியவற்றிற்கு ஒரே ஒரு நிழல் உரு \(16\).
மாறிலி சார்பு \(f(x) = 16\) என வரையறுக்கப்படுகிறது.
2. சமனிச் சார்பு:
\(f;A \rightarrow B\) என்ற சார்பு \(f(x)=x, x \in A\) என வரையறுக்கப்பட்டால் \(f\) ஆனது சமனிச் சார்பு ஆகும்.
Example:
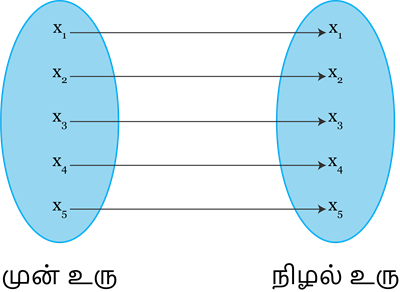
3. மெய் மதிப்புச் சார்பு
\(f : A \rightarrow B\) ஆனது மெய் மதிப்புச் சார்பு எனில்,\( f\)-யின் வீச்சகமானது, R எனும்
மெய்யெண்களின் உட்கணமாக இருக்கும்.
அதாவது, \(f(A) \subseteq R\).
Example:
மெய் சார்புக்கு சில எடுத்துக்காட்டுகள்:
1. \(f(x) = 3x - 8\)
2. \(f(x) = x^3\)
3. \(f(x) = \frac{2}{x}\)
Register for free to see more content